Las cargas puntuales son tan pequeñas que su tamaño no se considera mensurable, por eso se representan mediante un simple punto geométrico. La distancia que las separa es, por lo tanto, mucho mayor que sus dimensiones.
Es una idealización conveniente, ya que en muchas aplicaciones, las partículas subatómicas como los protones y los electrones pueden considerarse cargas puntuales, lo mismo que las moléculas cuando están ionizadas.
Coulomb realizó numerosos experimentos con cargas eléctricas consideradas puntuales, no tan pequeñas desde luego, como las partículas subatómicas, que no se conocerían hasta mucho tiempo después. Las esferitas cargadas que usaba Coulomb en sus experimentos tenían diámetros mucho menores que la separación entre ellas, cumpliendo la condición enunciada al principio.
Las cargas eléctricas se presentan de dos tipos: positivas, como los protones y negativas, como los electrones. Experimentalmente está comprobado que las cargas de signos iguales se repelen, mientras que las de signo contrario se atraen, una propiedad que se conocía desde la época de la Grecia antigua.
En sus experimentos, Coulomb varió las magnitudes de las cargas, así como su separación. Naturalmente encontró fuerzas de atracción y de repulsión, según los signos de las cargas.
Las observaciones de Charles Coulomb sobre las cargas eléctricas
Estas fueron las observaciones de Coulomb:
-La atracción o repulsión entre dos cargas puntuales q1 y q2 es directamente proporcional al producto de la magnitud de las cargas.
-La magnitud de la fuerza es inversamente proporcional al cuadrado de la separación entre las cargas.
-La fuerza siempre está dirigida a lo largo de la línea que une las cargas, se trata por lo tanto de una fuerza central.
Estas observaciones, puestas en una fórmula, conducen a la siguiente expresión:La fuerza es una magnitud vectorial, por lo tanto se denota con negrita. Las cargas q1 y q2, así como r, son escalares y r es el vector unitario en la dirección de la línea que une las cargas. Faltaría únicamente la constante de proporcionalidad, que transforma la expresión anterior en una igualdad.
Esta es la constante ke o simplemente k, llamada constante electrostática o constante de Coulomb.
Para dos cargas puntuales, la ley de Coulomb queda expresada formalmente por:
Es análoga a la ley de gravitación universal de Newton, claro que en este caso, las cargas pasan a ser las masas de los objetos y la constante de proporcionalidad es G, la constante de gravitación universal. La otra diferencia es que la fuerza de gravedad siempre es atractiva, mientras que la fuerza electrostática puede ser de atracción o repulsión según el signo de las cargas.
En cuanto a las unidades en el Sistema Internacional SI, son como sigue: la fuerza se expresa en newton (N), las cargas en culombios (C) en honor a Coulomb y la distancia 'r' en metros (m).
Por lo tanto, la constante electrostática viene en N.m2 / C2. Su valor se ha determinado experimentalmente y es aproximadamente de:
ke = 8.89 x 10 9 N.m2 / C2 ≈ 9 x 10 9 N.m2 / C2
En ocasiones se emplea la constante εo, llamada constante dieléctrica, de tal manera que:
El valor de εo es 8.85·10-12 C2 / N·m2.
El coulomb es una unidad bastante grande para las cargas, así que es necesario el uso de los submúltiplos. Los más frecuentes son:
-milicoulomb (mC) = 1 x10-3 C
-microcoulomb (μC) = 1 x10-6
C
-nanocoulomb (nC) = 1 x10-9
C
-picocoulomb (pC) = 1 x10-12 C
El principio de superposición
Cuando hay más de dos cargas interactuando, la fuerza neta sobre la carga qn viene dada por el principio de superposición:
Fneta = Fn1 + Fn2 + Fn3 + Fn4 + … = ∑ Fnj
Donde el subíndice j es 1, 2, 3, 4… y representa a las restantes cargas.
Ejercicios resueltos de la Ley de Coulomb
Cuando en el problema participan cargas puntuales, se aplica la ley de Coulomb como se ha establecido anteriormente, más el principio de superposición si hay más de dos cargas. Es preciso ser consistente con las unidades, ya que la constante electrostática ke viene dada casi siempre en unidades del Sistema Internacional, por lo tanto las distancias deben estar en metros y las cargas en coulombios.
Igualmente, la ley de Coulomb se aplica cuando se da por sentado que las cargas se encuentren en equilibrio estático.
Ejercicio 1
Dos cargas puntuales de + 5 x 10-6 C cada una, están separadas por una distancia de 0,01 m y se encuentran en equilibrio. ¿Que fuerza se ejerce sobre cada una de ellas?
Solución
Ya que las cargas son positivas, la
fuerza entre ellas es de repulsión. A las cargas se las ubica sobre un eje de
referencia, que puede ser el eje x, puesto que al ser la fuerza un vector, es
necesario indicar no solamente la magnitud, sino la dirección y el sentido. Y
la dirección, como se estableció previamente, es a lo largo de la línea que une
las cargas.
Sea F1 la fuerza que ejerce la carga 2 sobre la carga 1. Sustituyendo valores en la ley de Coulomb queda:
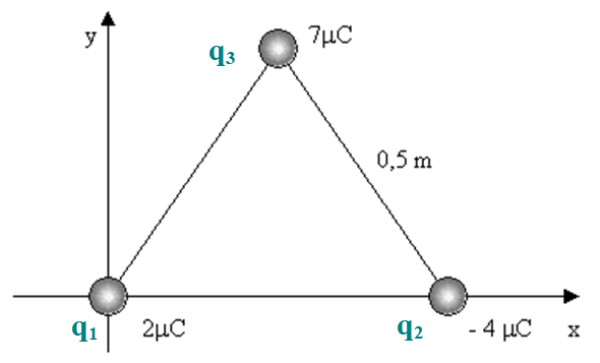
Figura 3. Tres cargas puntuales dispuestas en los vértices de un triángulo equilátero. Fuente: F. Zapata.
Es importante notar que la fuerza que la carga q2 ejerce sobre la carga q1 está dirigida en sentido negativo de las x, ya que es de repulsión.
En cuanto a la fuerza que q1 ejerce sobre q2, por ley de acción y reacción tiene la misma magnitud e igual dirección, pero sentido contrario. Por lo tanto:
F2 = 2250 (+i) N
Ejercicio 2
En la figura se muestran tres cargas puntuales ubicadas en los vértices de un triángulo equilátero. Calcular la fuerza eléctrica neta sobre la carga q3 = 7 mC.Solución
Sobre la carga q3 = 7 mC μC actúan dos fuerzas, que se muestran en el siguiente dibujo, que corresponde al diagrama de cuerpo libre de esta carga:
Por otro lado, la magnitud de F23 es el doble de la de F13, ya que la distancia entre todas las cargas es la misma, al estar ubicadas en los vértices de un triángulo equilátero.
Se ha dibujado un sistema de coordenadas cartesianas sobre la carga q3, ya que la fuerza resultante es un vector y es necesario expresarla con sus componentes. El ángulo entre la vertical y el lado del triángulo es 30º, ya que es un equilátero.
Dicho esto, el problema se resuelve fácilmente aplicando el principio de superposición y expresando las fuerzas a través de sus componentes a lo largo de los ejes x e y:
Fneta = F13+ F23
F13 = 0.252 i + 0.504 j N
F23 = 0.436 i − 0.872 j N
El vector Fneta se dibujó en verde en la figura, es un vector que pertenece al cuarto cuadrante. Su magnitud es:
El ángulo que dicha fuerza forma con el eje x es:
θ = arctg ( -0.436/0.756) = -30º
El signo (-) significa que este ángulo está medido desde el eje x positivo en sentido horario. Si se quiere medir el ángulo desde el eje x positivo en sentido antihorario, el ángulo sería 360º-30º = 330º.
Por F. Zapata.
No hay comentarios:
Publicar un comentario