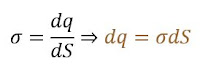Cómo calcular el campo eléctrico de una distribución continua de carga paso a paso

Cuando se tiene un objeto de tamaño mensurable, que además está provisto de carga eléctrica, se dice que se tiene una distribución de carga continua. El objeto puede ser un cable, una lámina, una esfera, un cilindro o, en general, cualquier objeto con tres dimensiones.

En realidad, se podría argumentar que la carga eléctrica está cuantizada, siendo la más pequeña posible, en la práctica, la del electrón, como es sabido. Sin embargo, para un objeto cargado con dimensiones mensurables, este hecho se puede ignorar, debido a la gran cantidad de electrones presentes.

La anguila eléctrica produce una descarga eléctrica que aturde a sus presas, gracias a que posee miles de células modificadas llamadas electrocitos, capaces de producir un campo eléctrico. Los seres humanos
también producen campos eléctricos mucho más débiles. Fuente de la imagen: Wikimedia Commons.

Procedimiento general

Para calcular el campo eléctrico que tal objeto produce en algún punto del espacio, conviene subdividirlo en cargas mucho más pequeñas. Tomando una sola de estas cargas, se puede considerar como una carga puntual y el campo que produce se halla a través de la ley de Coulomb para cargas puntuales.

El procedimiento se repite continuamente hasta hallar cada campo de cada carga puntual. Luego se suman, vectorialmente, y el resultado es el campo eléctrico total que la distribución produce en el punto seleccionado.

Si a una de estas cargas puntuales se la llama dq (diferencial de carga, el campo que ella produce en el punto P, situado a una distancia r, viene dado por:

En esta figura se tiene un objeto con carga total Q de forma arbitraria, del cual se toma una carga muy pequeña dq, ubicada en cualquier parte del mismo. La distancia entre dicha carga puntual y el punto donde se quiere calcular el campo es r, mientras que k es la constante electrostática:

k ≈ 8.9875517873681764 × 10⁹ N·m²/C²≈ 9 × 10⁹ N·m²/C²

 Se puede resumir esta estrategia de cálculo en los siguientes puntos:

• Se ‘divide’ matemáticamente el objeto en numerosas cargas minúsculas, que pueden considerarse ‘puntuales’.
• Enseguida, se aplica a cada una de estas cargas, llamadas dq, la ley de Coulomb para el campo eléctrico.
• Por último, se suman vectorialmente todos los campos eléctricos así obtenidos, lo cual se hace estableciendo una integral definida sobre toda la distribución y resolviéndola.

Este es el procedimiento general que se sigue para calcular cualquiera problema de campo eléctrico en una distribución continua.

La dificultad radica, por supuesto, en establecer y resolver la integral correcta. Esta solo puede resolverse analíticamente en ciertos casos con gran simetría, del resto, se resuelve mediante procedimientos numéricos.

Además, nunca se debe olvidar que el campo eléctrico es un vector, y que, por lo tanto, hay que estar atento a dar todas sus componentes.

Vamos a desarrollar un ejemplo con el que esperamos clarificar la cuestión de cómo plantear y resolver la integral, ya que este el punto que suele presentar más dificultades.

 

Ejemplo resuelto paso a paso

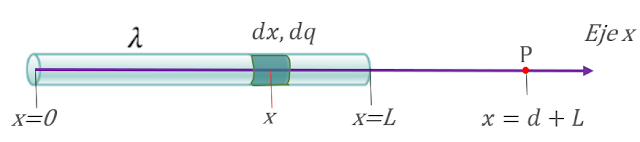
Calcular el campo eléctrico producido por una barra delgada de longitud L, cargada uniformemente con carga total Q, en el punto P mostrado en la figura, el cual dista una distancia d del extremo derecho de la barra:

Solución

Paso 1

El primer paso es establecer un sistema de referencia para ubicar correctamente tanto la distribución de carga como el punto donde se quiere calcular el campo. En este ejemplo, basta con situarlo todo sobre el eje x, entonces, el extremo izquierdo de la barra está x=0, el extremo derecho en x=L y el punto P en la posición x=d+L.

Paso 2

Una vez situado el sistema de referencia con todo lo que indica el enunciado, es el momento de tomar el dq que se va a colocar en la ley de Coulomb. ¿Dónde se tomará? Pues en cualquier parte de la distribución, evitando hacerlo en mitad de ella o en un extremo, ya que esta carga diferencial debe estar en un lugar arbitrario.

En la figura, esta ubicación se ha marcado en rojo y se la denota simplemente como x. Todo lo que se sabe de ella es que se encuentra entre x=0 y x=L. A la carga puntual en cuestión la hemos resaltado con un color más oscuro.

 

Paso 3

El siguiente paso es relacionar la carga puntual dq con la geometría de la distribución, a través de alguna expresión algebraica. Como el enunciado afirma que la carga está uniformemente distribuida sobre la barra, entonces simplemente:

Q=λ∙L

Y, en consecuencia:

dq=λ∙dx

Es decir, cuando la carga total Q se distribuye de forma homogénea en toda la longitud L de la barra, lógicamente también será así si una carga dq se distribuye a lo largo de una longitud infinitesimal dx.

 

Paso 4

Ahora vienen los cálculos con la ley de Coulomb, donde se va a sustituir todo lo que se estableció en los pasos previos, pero antes, es preciso esbozar el campo producido por la carga infinitesimal dq.

Dado que el enunciado informa que la carga de la barra es Q, positiva, el campo dE es saliente a la barra y dirigido a lo largo de la línea que une a dq con P:

El vector se ha destacado en color azul para mayor claridad. Por lo tanto, el campo estará dirigido a lo largo del eje x en sentido positivo.

Todo está listo para calcular la integral:

Recuérdese que la distancia r es la que hay entre la carga infinitesimalmente pequeña y el punto P donde se desea calcular el campo. Se ha resaltado en la figura de arriba como r= d+L-x.

Paso 5

En este paso, se integra sobre toda la distribución de carga y se resuelve la integral. Obsérvese que la variable de integración es “x” y que varía desde x=0 hasta x=L, es decir, se integra por toda la extensión de la barra. La integral dará el campo eléctrico total en el punto P:

Haciendo el cambio de variable:

u =d+L-x; du = -dx

Cuando x=0, u=d+L y cuando x=L, u = d, la se transforma en:

En ocasiones, es conveniente expresar el resultado en términos de la carga total Q presente en la barra, en vez de la densidad de carga. Entonces, sabiendo que Q=λ∙L:

Paso 6

Verificar la ecuación obtenida desde el punto de vista de las dimensiones.

La expresión para cualquier campo eléctrico, en unidades del Sistema Internacional, contiene:

• La constante electrostática k, o bien la equivalente en términos de la permitividad del vacío ε₀, sabiendo que k = 1 / (4πε₀) y ε₀ ≈ 8.854 × 10⁻¹² C²/N·m².
• Carga eléctrica en el numerador.
• Una distancia al cuadrado en el denominador.

Según esto, la ecuación que se obtuvo en el paso 5 es correcta desde el punto de vista dimensional.

Otra forma de verificar que la ecuación es correcta es hacer tender L a 0 (¿por qué?) y ver que se obtiene la expresión para el campo eléctrico producido por una carga puntual:

Resumen

Cuando se tiene una distribución de carga continua y se quiere el calcular el campo que produce en cualquier punto P, hay que:

• Establecer un sistema de referencia adecuado.
• Dividir la distribución en pequeñas cargas infinitesimales.
• Expresar el diferencial de carga en términos de la densidad de carga y la geometría de la distribución.
• Armar la integral, cuyos límites estarán dados por la geometría de la distribución y recordando que el campo eléctrico es un vector, por lo que, en principio, habrá una integral por cada componente.
• Aprovechar las simetrías, si las hay, con el fin de facilitar y simplificar los cálculos. Por ejemplo, el campo de una distribución de carga esférica debe ser radial.
• Aplicar un método para la resolución de la integral. Si la distribución carece de simetría, un método numérico siempre será de utilidad.

Por F. Zapata.

Distribuciones de carga continua

Se dice que los objetos de tamaño mensurable con carga eléctrica son distribuciones de carga continua. Tales distribuciones deben tener, al menos, una dimensión medible o mensurable.

Recuérdese que en post anteriores, se ha hecho referencia a las ‘cargas puntuales’, las cuales son cargas eléctricas tan, pero tan pequeñas, que no se requiere tener en cuenta sus dimensiones. Pero en el caso de las distribuciones continuas, el tamaño sí importa.

Un alambre delgado cargado eléctricamente es una distribución de carga continua. Fuente: Flickr.

La distribución de carga continua más simple es el alambre o la varilla delgada cargada eléctricamente. La carga puede distribuirse de manera equitativa a lo largo de toda la longitud, o bien puede seguir alguna distribución particular, como por ejemplo, concentrarse más en un extremo del alambre y menos en el otro, o concentrarse en el centro.

En cada caso, el campo eléctrico producido por dicha distribución será diferente, dependiendo de la ubicación de la carga y el punto donde se quiera calcular el campo. Por ejemplo, si la varilla o alambre tiene carga uniformemente distribuida, y el punto de interés se localiza en el eje del alambre, a cierta distancia de un extremo, no será igual el campo que produce allí el extremo más cercano del alambre, que el que produce el extremo más lejano, como es lógico.

El extremo más lejano produce un campo menos intenso, en razón de su lejanía, mientras que el extremo más cercano produce un campo más intenso.

La pregunta que surge es: ¿cómo tener en cuenta estas diferencias a la hora de calcular el campo eléctrico? Después de todo, la ley de Coulomb se define, en principio, para cargas puntuales, por lo tanto, ¿cómo se la puede aplicar para calcular el campo eléctrico de un objeto continuo en un punto dado?

 

Estrategia para calcular el campo eléctrico de una distribución continua

Es tan simple que se puede resumir en tres pasos:

• Se ‘divide’ (matemáticamente, claro está) el objeto en multitud de cargas minúsculas, que pueden considerarse ‘puntuales’.
• Se aplica a cada una de estas cargas la bien conocida ley de Coulomb para el campo eléctrico.
• Finalmente, se suman (vectorialmente) todos los campos eléctricos así obtenidos (¡hay que resolver una integral!) y ya se tiene por fin el campo eléctrico resultante en el punto en cuestión.

Ahora, hagamos un gráfico que ilustre lo antes dicho. Se tiene un objeto con carga eléctrica Q, distribuida sobre él, la cual, por comodidad, se supondrá positiva. El objeto tiene una forma arbitraria.

Se toma una pequeña porción del objeto, que contiene una pequeñísima porción de carga, la cual se llamará dq. Este será nuestro diferencial de carga, representado por el cubito en la parte superior del objeto en la figura de abajo.

Luego se elige un punto P en los alrededores, que dista una determinada distancia r de dq. Allí, nuestra dq produce en P una pequeña contribución del campo eléctrico dE, la cual se puede calcular a través de la ley de Coulomb para cargas puntuales:

Recuérdese que el campo eléctrico es un vector, de allí que es necesario especificar siempre su dirección, por eso se requiere escribir siempre el vector unitario respectivo. En el caso de una distribución de carga positiva, el campo es saliente, mientras que si es negativa, el campo es entrante a la misma.

Esquema de la aplicación de la ley de Coulomb para el campo eléctrico en una distribución de carga continua.

El campo eléctrico resultante en P, producido por todas las pequeñas contribuciones ubicadas en los distintos lugares del objeto, hasta cubrirlo por completo, es la integral efectuada sobre todo el volumen V del objeto.

Si el objeto no tiene un volumen apreciable, pero sí una superficie S mensurable, la integral se hará sobre dicha superficie:

Por último, si la dimensión mensurable del objeto es su longitud L, como en el caso del alambre mencionado al comienzo, la integral se llevará a cabo sobre dicha longitud.

Este es el procedimiento general para trabajar con distribuciones de carga continua, ya que cada caso tendrá su propia geometría, es decir, unos determinados dq y un r, los cuales deberán expresarse convenientemente para poder calcular la respectiva integral y obtener el campo.  

 

Densidades de carga eléctrica

El concepto de densidad de carga, análogo al ya familiar de densidad de masa, ayudará a establecer el dq apropiado para calcular la integral del campo eléctrico.

En esta imagen se resumen las tres posibilidades geométricas discutidas en el apartado anterior: distribución lineal de carga, con una densidad de carga lineal, distribución superficial de carga, con una densidad de carga superficial y, por último, la distribución de carga volumétrica, son su densidad de carga volumétrica.

Fuente: hyperphysics.

Se han elegido letras griegas para simbolizar a cada densidad de carga, como se explica seguidamente:

Densidad de carga lineal

Se representa como λ, cuyas unidades son culombios por metro (C/m)

En este caso:

→ Cálculo de la carga total

En ocasiones, es preciso calcular la carga total Q distribuida sobre el alambre.

• Si la densidad es uniforme, el cálculo es muy simple:

Q=λ∙L

• Si la densidad es no uniforme, sino que depende de alguna coordenada espacial, digamos ‘x’, entonces hay que integrar sobre dicha dimensión, tomando una longitud infinitesimal sobre el alambre, dada por dx:

Donde L representa la longitud total del alambre.

 

Densidad de carga superficial

Se representa mediante σ, cuyas unidades son culombios por metro cuadrado (C/m²)

En este caso:

     

• ‘dS’ es una superficie infinitesimal
•  σ puede ser uniforme, o bien ser una función de las coordenadas espaciales.

 

→ Cálculo de la carga total

• Si la densidad es uniforme:

Q=σ∙S

• Si la densidad es no uniforme, sino que depende de las coordenadas espaciales, digamos ‘x’ e ‘y’, entonces hay que integrar sobre la superficie S:

Donde dS representa una superficie muy pequeña del objeto (infinitesimal).

 

Densidad de carga volumétrica

Se la denota como ρ, cuyas unidades son culombios por metro cúbico (C/m³).

En este caso:

• ‘dV’ es un volumen infinitesimal
• ρ puede ser uniforme, o bien ser una función de las coordenadas espaciales.

→ Cálculo de la carga total

• Si la densidad es uniforme:

Q=ρ∙V

• Si la densidad es no uniforme, sino que depende de las coordenadas espaciales, sino que depende de las coordenadas espaciales ‘x’, ‘y’ y ‘z’, por ejemplo, entonces hay que integrar sobre el volumen V:

Ejemplo 1

Distribución superficial de carga uniforme

Se tiene un disco de 5 cm de radio, con carga eléctrica positiva distribuida de manera uniforme en su superficie a razón de 1.2 × 10^-7 C/m². ¿Cuál es la carga total Q almacenada en el disco?

Solución

Dado que la carga está distribuida de manera uniforme sobre el disco, la carga total es directamente el producto de la densidad de carga superficial y el área del disco:

El área del disco es simplemente S =πr²:

S =πr² = π × (5×10^-2 m)² = 0.0079 m²

Sabiendo que σ = 1.2 × 10^-7 C/m², la carga total guardada en el disco es:

Q=σ∙S = 1.2 × 10^-7 C/m² × 0.0079 m² = 9.5 × 10^-10 C.

Ejemplo 2

Distribución lineal de carga no uniforme

Se tiene un alambre de longitud L = 1.5 m, el cual tiene una densidad de carga dada por:

¿Cuál es la carga total en el alambre?

Solución

La carga no está distribuida uniformemente, sino que depende de la ubicación ‘x’ de cada punto sobre el alambre. Si colocamos un sistema de referencia donde el alambre se ubica sobre el eje horizontal (el eje x), y los tonos de gris representan la carga, en x=0 será blanco (porque no hay carga) mientras que en x = 1.5 m la densidad de carga será máxima, por eso se ve en negro.

Un segmento arbitrario dx, que contiene una pequeña carga dq, ubicado en un lugar arbitrario del alambre, tendrá una densidad de carga intermedia. La figura servirá luego para calcular el campo eléctrico del alambre, pero eso queda para otro post.

Ahora vamos al cálculo de la carga total, que es muy simple:

Por F. Zapata.

Ley de Coulomb para cargas puntuales: 6 ejercicios resueltos con solución detallada

 

Ejercicio 1 

Cargas eléctricas

La electricidad estática común involucra cargas que oscilan entre nano culombios y micro culombios. Determinar

a) La cantidad de electrones necesarios para formar una carga de −2,00 nC

b) ¿Cuántos electrones se deben eliminar de un objeto neutro para dejar una carga neta de 0,500 μC?

 

Solución a

Sabiendo que la carga eléctrica de un electrón tiene carga de −1.6×10⁻¹⁹ C, y que 1 nC=1 ×1 0⁻⁹ C, se tiene que:

−2,00 nC = −2 ×1 0⁻⁹ C

Solución b

Se tiene la siguiente equivalencia:

1 μC=1 ×1 0⁻⁶ C

Por lo tanto:

0.5 μC=0.5 ×1 0⁻⁶ C

Entonces:

Ejercicio 2 

Cargas eléctricas en una dimensión

Dos cargas de igual magnitud y de distinto signo se encuentran en el vacío, separadas una distancia de 50 centímetros. Se sabe que la magnitud de la fuerza eléctrica de atracción entre ellas es 0,9 N. ¿Cuál es la magnitud de las cargas?

Solución 

La magnitud de la fuerza de atracción entre las cargas es:

Donde q₁ y q₂ son las magnitudes de las cargas, k es la constante electrostática 9×10⁹  N•m²/C² y r la separación entre las cargas. Como las cargas tienen igual magnitud:

q₁ = q₂= Q

Reemplazando esta condición y despejando Q en la ley de Coulomb, se obtiene:

Ejercicio 3

Cargas puntuales en equilibrio electrostático

 

Sobre una línea recta se disponen tres partículas cargadas separadas por una distancia d, como se muestra en la figura. Las cargas q₁ y q₂, de distinta magnitud y signos opuestos, se mantienen fijas, mientras que una tercera carga positiva q₃ puede moverse libremente sobre la línea que las une.

¿Dónde se debe ubicar q₃  para que permanezca en equilibrio electrostático, suponiendo que la magnitud de q₂ es mayor que la de q₁?

Solución 

Sea F₁₃ la fuerza que ejerce la carga q₁ sobre la carga q₃. Al ser del mismo signo, dicha fuerza es de repulsión, en cambio, la fuerza F₂₃ es de atracción, por ser q₂ y q₃ de distinto signo. Para que q₃ se encuentre en equilibrio, la magnitud de dichas fuerzas debe ser la misma.

Para que la carga q₃ permanezca en equilibrio estático, debe colocarse a la izquierda de q₁, a cierta distancia x, ya que la magnitud de q₁ es menor que la de q₂.

Nótese que si se colocara a q₃ en medio de las otras dos cargas, la fuerza resultante estaría dirigida de izquierda a derecha, por lo que sería imposible lograr que quedara en equilibrio estático, mientras que si q₃ se colocara a la derecha de q₂, por ser esta de mayor magnitud, la fuerza F₁₃ no tendría forma de equilibrarla.

Ejercicio 4 

Cargas puntuales en equilibrio electrostático

Para el sistema de tres cargas puntuales del ejercicio 3, determinar una expresión para el valor de x, la distancia a la cual se debe colocar la carga q₃ de la carga q₁ para que se encuentre en equilibrio estático.

Solución

Partiendo de:

Se tiene que:

Por lo tanto, para que las cargas se encuentren en equilibrio electrostático, debe cumplirse que la fuerza neta se anule. Como ambas fuerzas tienen la misma dirección y sentidos opuestos, se puede prescindir de la notación vectorial e igualar sus magnitudes:

Esta es una ecuación de segundo grado, que se resuelve mediante la fórmula cuadrática:

Con:

a= q₁— q₂

b= 2dq₁

c= q₁d²

Enseguida, se sustituye cuidadosamente los términos anteriores en la ecuación cuadrática, teniendo presente que la incógnita siempre es “x”. Es importante destacar que la ecuación cuadrática tiene al menos dos soluciones, pero en este caso, se escogerá la que tenga el signo + como resultado, ya que una distancia siempre es positiva.

Ejercicio 5 

Cargas puntuales en equilibrio electrostático en dos dimensiones

Las cargas puntuales q₁ = +0.2μC ; q₂ = −0.4μC y q₃ = -0.1μC se disponen según el triángulo de la figura. Calcular la fuerza resultante sobre la carga q₁.

Solución

Se dibuja el diagrama de cuerpo libre sobre la carga q₁, seleccionando un sistema de coordenadas cartesianas adecuado:

F₁₂ (rojo) es la fuerza de atracción entre q₁ y q₂, F₁₃ (verde), es la fuerza de atracción entre q₁ y q₃. El diagrama no está necesariamente a escala.

La fuerza neta sobre q₁  es:

F_neta = F₁₂ + F₁₃

De acuerdo al sistema de referencia seleccionado, la fuerza F₁₂ tiene componentes:

F_12x = F₁₂∙senθ = F₁₂∙(4/5)= 0.8F₁₂

F_12y = F₁₂∙cosθ = F₁₂∙(3/5)= −0.6F₁₂

Por su parte, la fuerza F₁₃ está verticalmente dirigida hacia abajo, entonces:

F_neta = F₁₂ + F₁₃ = 0.8F₁₂ i + (−0.6F₁₂ − F₁₃) j

Nótese la distinción entre vectores (en negrita) y sus magnitudes. Ahora estas se pueden calcular con la ley de Coulomb:

F_neta = F₁₂ + F₁₃ = 0.8×8.64×10⁻⁵ i + (−0.6×8.64×10⁻⁵ − 2.00×10⁻⁵) j = (−6.9 i − 7.2 j) ×10⁻⁵ N

Ejercicio 6

Fuerza eléctrica entre cargas puntuales y segunda ley de Newton

Dos bolitas, cada una de 5,0 g de masa, están atadas a hilos de seda de 50 cm de longitud, que a su vez están atados al mismo punto del techo, como se muestra en la figura. Cuando las bolitas tienen la misma carga Q, los hilos cuelgan a 5,0° respecto a la vertical, como se muestra en la figura. Determinar:

a)    La magnitud de Q

b) ¿Qué puede decirse de los signos de las dos cargas?

Solución a

En primer lugar, se dibuja un diagrama de cuerpo libre de una de las bolitas, con el fin de aplicar la segunda ley de Newton. Las bolitas se encuentran en equilibrio estático.

Tres fuerzas actúan sobre cualquiera de las bolitas:

• La tensión en la cuerda T, que forma un ángulo de 5º con la vertical.
• La fuerza de repulsión electrostática F_e
• El peso W

Ya que la tensión T está inclinada respecto al eje y, tiene dos componentes, una vertical, llamada T_y, y otra horizontal T_x, en consecuencia, al aplicar la segunda ley de Newton, se obtiene:

∑ F_y =T_y – W = 0

∑ F_x =F_e – T_x = 0

De la primera ecuación:

T_y = W ⇨ T∙cos 5º = mg

Y de la segunda:

F_e – T_x = 0 ⇨ F_e = T∙sen 5º

Por lo tanto:

La ley de Coulomb afirma que:

Siendo q₁ y q₂ las magnitudes de las cargas, k la constante electrostática 9×10⁹  N•m²/C² y r la separación entre las cargas. Del esquema es fácil verificar, mediante trigonometría elemental, que la distancia entre las cargas es:

r = 2d = 2L∙sen 5º

Donde L es la longitud de la cuerda, igual a 50 cm o 0.5 m.

Como las bolitas son idénticas, q₁ = q₂= Q. Al sustituir en la expresión antes deducida para F_e, resulta:

Importante: Antes de sustituir valores numéricos, es necesario asegurarse de que todas las cantidades, tales como longitudes, masas, etc., se encuentren en unidades del Sistema Internacional.

Solución b

Con la información suministrada no es posible determinar si ambas cargas son positivas o negativas, lo que sí es seguro es que son del mismo signo.

Por F. Zapata

¿Tienes dudas o necesitas más ejemplos resueltos? 

¡Podemos ayudarte! 

Déjanos un mensaje y te responderemos a la brevedad. Te brindamos asesorías personalizadas por WhatsApp y Telegram a precios solidarios:

 +058 412 7110460 

Aceptamos Paypal, Payoneer y transferencia bancaria (en este último caso solo bancos de Venezuela y Argentina).