El límite de Roche es la distancia mínima a la que puede orbitar un objeto a otro, sin que la atracción gravitatoria de este lo fragmente en pedazos. Su valor está vinculado a las fuerzas de marea, que determinan no solamente la aparición de las mareas oceánicas en la Tierra, sino también la forma de las órbitas y las deformaciones que sufren los cuerpos celestes, entre otros efectos.
Las fuerzas de marea se deben a la interacción gravitatoria diferencial que se origina por la diferencia de tamaño entre los cuerpos. Al ser diferente la fuerza que siente cada punto de un objeto, este se distorsiona, de tal manera que si inicialmente era esférico, tenderá a volverse elipsoidal. |
| La Luna es la principal responsable de las mareas oceánicas en la Tierra. Fuente: Pixahive. |
Como los gases y los líquidos son más susceptibles de ser deformados, este efecto diferencial de la gravedad es responsable no solo de las conocidas mareas oceánicas, sino también de las mareas atmosféricas.
Pero, aunque no parezca posible, la parte rocosa de la Tierra también se ve afectada por la fuerza de marea en menor medida, ocasionando las llamadas mareas terrestres, en las que, en algunos casos, la corteza puede elevarse hasta 50 cm.
La Luna es el principal causante de las mareas oceánicas, y también el Sol, en menor medida. Por supuesto, la Luna también se ve afectada por las fuerzas de marea causadas por la Tierra, aunque no tenga océanos.
A modo de ejemplo, las fuerzas de marea causadas por la tierra han provocado la desaceleración del satélite, de manera que el tiempo que tarda en dar una vuelta a la Tierra y el tiempo que tarda en girar una vuelta sobre sí misma han terminado por igualarse, dando como resultado que siempre muestre la misma cara hacia nosotros.
El Sol, por su parte, también ejerce una fuerza de marea sobre la Tierra, pero a pesar de ser muchísimo mayor que la Luna, sus efectos no son tan notables, porque se encuentra bastante más alejado.
Cálculo de la expresión para la fuerza de marea diferencial
Para encontrar una expresión matemática de la fuerza de
marea diferencial, nos podemos valer del esquema que se muestra a continuación,
donde se muestra una situación simplificada en la que únicamente interactúan la
Tierra y la Luna a través de la gravedad. Otras fuerzas se excluyen y tanto la
Tierra como la Luna son esféricas e indeformables.
En el siguiente dibujo, m1 y m2 son dos puntos de la Tierra situados diametralmente opuestos, por lo tanto, la atracción gravitatoria que la Luna ejerce sobre ellos es diferente, siendo mayor en el punto más cercano a ella, y menor en el punto más alejado, lo cual se ha representado con flechas de distinto tamaño.
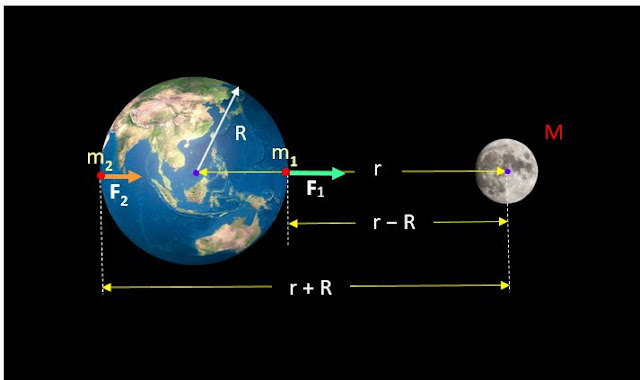 |
| Fuente: F. Zapata. |
Por otro lado, el radio de la Tierra es ‘R’ y la distancia
entre los centros de la Tierra y la Luna es ‘r’.
Para calcular la gravedad entre la Luna y cada uno de los puntos, se emplea la conocida ecuación hallada por Newton:
Donde F representa el vector fuerza, M es la masa de la luna, concentrada en su centro, m es la masa de cada punto, que se supondrán idénticas por simplicidad, d es la distancia que separa a M de cada una de las masas puntuales, G es la constante de gravitación universal, cuyo valor es G = 6.673 × 10−11 N∙m2/kg2 y, por último, el vector unitario a la extrema derecha representa la dirección de la línea que une las masas con el centro de la Luna.
El carácter vectorial de la fuerza no
será un problema, ya que las fuerzas están en la misma dirección y tienen el
mismo sentido, como se ve del dibujo.
Su diferencia es lo que se conoce como fuerza
de marea y se denota como ΔF. Para encontrarla, simplemente
basta con efectuar la resta:
ΔF = F2 – F1
Sea ΔF la magnitud de la fuerza diferencial en el
esquema:
Puesto que las masas de cada punto son idénticas, se
puede factorizar la expresión de esta forma:
Ahora bien, la distancia r es
mucho mayor que el radio R, o lo que es igual, la distancia que separa
los centros de la Tierra y de la Luna (384.400 km), es mucho mayor que el radio
de la Tierra (6371 km).
Esto permite hacer una aproximación que
simplifique la expresión, si se emplea la expresión equivalente:
Ahora un poco más de matemáticas,
¡paciencia!
Se utilizarán los siguientes desarrollos en serie de potencias, que se pueden obtener fácilmente en páginas como Wolfram Alpha:
Dado que:
Las potencias mayores o iguales que 2
resultan muy pequeñas y no es necesario tomarlas en cuenta, por lo tanto:
Gracias a lo anterior, se reescribe ΔF como sigue:
Y la fuerza de marea diferencial máxima, causada
por la Luna sobre la Tierra, se expresa, de forma aproximada como:
Nótese que la fuerza diferencial de marea decae con la distancia mucho más rápidamente que la fuerza de gravedad.
Estimación del límite de Roche
Ahora sí, estamos listos para estimar el
límite de Roche a través de la fuerza diferencial máxima de marea y el problema
es el siguiente:
Si
no se quiere que la Luna se fragmente, ¿a qué distancia mínima ‘r’ debe estar
de la Tierra?
Respuesta: la Luna sufrirá una perturbación debida a las fuerzas de marea que ejerce la Tierra sobre ella, si la atracción gravitatoria producida por el centro de la Luna sobre el punto de su superficie más cercano a la Tierra es menor que la aceleración gravitatoria diferencial hacia el exterior, producida sobre dicho punto por la Tierra.
Con la ayuda del siguiente esquema:
La fuerza diferencial en este caso es:
Donde ML es la masa de
la Luna, MT es la masa de la Tierra, RL es
el radio de la Luna, r es la distancia entre los centros de la Luna y de
la Tierra y G es la constante de gravitación universal.
Por lo tanto, este punto de masa m
sobre la superficie de la Luna experimenta una aceleración de marea equivalente
a:
Mientras que experimenta una aceleración
de gravedad lunar igual a:
Puesto que se ha supuesto que la gravedad
es la única fuerza que cohesiona las partículas, la Luna se fragmentará si dicha
aceleración de gravedad es menor en magnitud que la aceleración de marea:
ML = 7,349 × 1022 kg
MT = 5,972 × 1024 kg
RL = 1.737,4 km
Con estas condiciones, el límite de Roche
para la Luna es de 9483 km, lo cual significa que, si su órbita la llevara a
acercarse a la Tierra a una distancia menor, las fuerzas de marea la
fragmentarían inevitablemente.
Afortunadamente, la distancia promedio
entre la Tierra y la Luna es 384402 km aproximadamente, por lo cual nuestro
satélite está a salvo.
El modelo anterior es demasiado
simplista, así que el astrónomo Roche llevó a cabo un cálculo en el que supuso la
existencia de la deformación, el hecho de que los objetos no son esferas
perfectas sino esferoides y que, además, tienen rotación sobre sí mismos.
Con este nuevo modelo y empleando
análisis numérico, el límite de Roche se calcula con mayor precisión, dando
lugar al coeficiente de 2.456 en vez de 1.26:
En vez de utilizar las masas de los respectivos objetos, el límite de Roche se calcula preferentemente con la densidad. En tal caso, se escribe como sigue:
Quaoar, el objeto transneptuniano con un peculiar sistema de anillos
Hasta la fecha, cuerpos celestes del Sistema Solar, tales como satélites y anillos planetarios, cumplen con el límite de Roche. En particular, los anillos de los planetas gigantes se encuentran muy cercanos al límite de Roche, aunque fuera de la zona de peligro.
Sin embargo, recientemente se ha dado a conocer que el objeto transneptuniano Quaoar posee un sistema de anillos que se encuentra mucho más alejado de su límite de Roche, donde, en teoría, no deberían encontrarse los anillos, sino un satélite.
 |
| Impresión artística de Quaoar y sus insólitos anillos. Fuente: Wikimedia Commons. |
De la discusión anterior, queda claro que el límite de Roche solamente considera a la fuerza gravitacional como la fuerza que cohesiona a los objetos celestes.
No obstante, un satélite artificial puede orbitar tranquilamente a la Tierra muy por debajo del límite de Roche, sin que la fuerza de marea lo fragmente en pedazos. Esto se debe a que el satélite puede vencer a las fuerzas de marea gracias a los tornillos, pernos y soldaduras que le dan forma. Nuestros cuerpos, ni tampoco los objetos que nos rodean, son dispersados por las fuerzas de marea, ya que nuestra cohesión depende principalmente de fuerzas electromagnéticas.
Entonces, ¿qué otras fuerzas intervienen en Quaoar, además de la gravedad, para permitirle tener anillos en un lugar donde no deberían estar?
Todavía los científicos no lo saben, sin embargo, trabajan afanosamente en busca de información que les permita explicar un hecho tan desconcertante.
Por F. Zapata
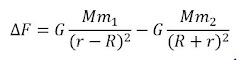









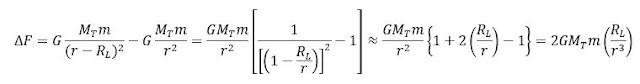















.jpg)