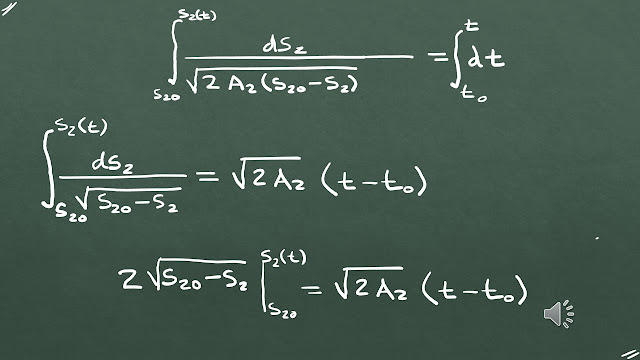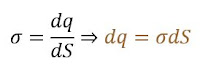Bloque sobre cuña deslizante

 Aplicación del principio de Conservación de la Energía y del momentum lineal

Solución paso a paso

En esta entrada se resuelve, paso a paso, el problema del bloque que se coloca sobre un plano inclinado deslizante (en forma de cuña).

Se supone que todas las superficies son perfectamente lisas, debido a lo cual se conserva la energía mecánica del sistema, así como la componente horizontal del momentum lineal.

Partiendo de estos dos grandes principios se obtienen expresiones algebraicas explicitas para las velocidades del bloque y la cuña, como función de la posición.

Asimismo, también se obtienen las expresiones exactas que dan la posición de ambos objetos como función del tiempo.

Adicionalmente, se usan las expresiones obtenidas para simular, mediante GeoGebra, el movimiento del sistema.

VIDEO (AL FINAL DE LA ENTRADA)

VIDEO:

Cómo calcular el campo eléctrico de una distribución continua de carga paso a paso

Cuando se tiene un objeto de tamaño mensurable, que además está provisto de carga eléctrica, se dice que se tiene una distribución de carga continua. El objeto puede ser un cable, una lámina, una esfera, un cilindro o, en general, cualquier objeto con tres dimensiones.

En realidad, se podría argumentar que la carga eléctrica está cuantizada, siendo la más pequeña posible, en la práctica, la del electrón, como es sabido. Sin embargo, para un objeto cargado con dimensiones mensurables, este hecho se puede ignorar, debido a la gran cantidad de electrones presentes.

La anguila eléctrica produce una descarga eléctrica que aturde a sus presas, gracias a que posee miles de células modificadas llamadas electrocitos, capaces de producir un campo eléctrico. Los seres humanos
también producen campos eléctricos mucho más débiles. Fuente de la imagen: Wikimedia Commons.

Procedimiento general

Para calcular el campo eléctrico que tal objeto produce en algún punto del espacio, conviene subdividirlo en cargas mucho más pequeñas. Tomando una sola de estas cargas, se puede considerar como una carga puntual y el campo que produce se halla a través de la ley de Coulomb para cargas puntuales.

El procedimiento se repite continuamente hasta hallar cada campo de cada carga puntual. Luego se suman, vectorialmente, y el resultado es el campo eléctrico total que la distribución produce en el punto seleccionado.

Si a una de estas cargas puntuales se la llama dq (diferencial de carga, el campo que ella produce en el punto P, situado a una distancia r, viene dado por:

En esta figura se tiene un objeto con carga total Q de forma arbitraria, del cual se toma una carga muy pequeña dq, ubicada en cualquier parte del mismo. La distancia entre dicha carga puntual y el punto donde se quiere calcular el campo es r, mientras que k es la constante electrostática:

k ≈ 8.9875517873681764 × 10⁹ N·m²/C²≈ 9 × 10⁹ N·m²/C²

 Se puede resumir esta estrategia de cálculo en los siguientes puntos:

• Se ‘divide’ matemáticamente el objeto en numerosas cargas minúsculas, que pueden considerarse ‘puntuales’.
• Enseguida, se aplica a cada una de estas cargas, llamadas dq, la ley de Coulomb para el campo eléctrico.
• Por último, se suman vectorialmente todos los campos eléctricos así obtenidos, lo cual se hace estableciendo una integral definida sobre toda la distribución y resolviéndola.

Este es el procedimiento general que se sigue para calcular cualquiera problema de campo eléctrico en una distribución continua.

La dificultad radica, por supuesto, en establecer y resolver la integral correcta. Esta solo puede resolverse analíticamente en ciertos casos con gran simetría, del resto, se resuelve mediante procedimientos numéricos.

Además, nunca se debe olvidar que el campo eléctrico es un vector, y que, por lo tanto, hay que estar atento a dar todas sus componentes.

Vamos a desarrollar un ejemplo con el que esperamos clarificar la cuestión de cómo plantear y resolver la integral, ya que este el punto que suele presentar más dificultades.

 

Ejemplo resuelto paso a paso

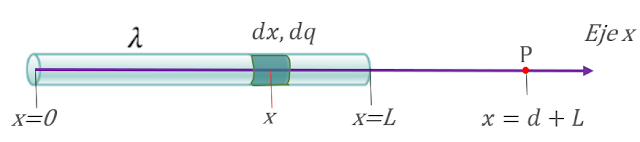
Calcular el campo eléctrico producido por una barra delgada de longitud L, cargada uniformemente con carga total Q, en el punto P mostrado en la figura, el cual dista una distancia d del extremo derecho de la barra:

Solución

Paso 1

El primer paso es establecer un sistema de referencia para ubicar correctamente tanto la distribución de carga como el punto donde se quiere calcular el campo. En este ejemplo, basta con situarlo todo sobre el eje x, entonces, el extremo izquierdo de la barra está x=0, el extremo derecho en x=L y el punto P en la posición x=d+L.

Paso 2

Una vez situado el sistema de referencia con todo lo que indica el enunciado, es el momento de tomar el dq que se va a colocar en la ley de Coulomb. ¿Dónde se tomará? Pues en cualquier parte de la distribución, evitando hacerlo en mitad de ella o en un extremo, ya que esta carga diferencial debe estar en un lugar arbitrario.

En la figura, esta ubicación se ha marcado en rojo y se la denota simplemente como x. Todo lo que se sabe de ella es que se encuentra entre x=0 y x=L. A la carga puntual en cuestión la hemos resaltado con un color más oscuro.

 

Paso 3

El siguiente paso es relacionar la carga puntual dq con la geometría de la distribución, a través de alguna expresión algebraica. Como el enunciado afirma que la carga está uniformemente distribuida sobre la barra, entonces simplemente:

Q=λ∙L

Y, en consecuencia:

dq=λ∙dx

Es decir, cuando la carga total Q se distribuye de forma homogénea en toda la longitud L de la barra, lógicamente también será así si una carga dq se distribuye a lo largo de una longitud infinitesimal dx.

 

Paso 4

Ahora vienen los cálculos con la ley de Coulomb, donde se va a sustituir todo lo que se estableció en los pasos previos, pero antes, es preciso esbozar el campo producido por la carga infinitesimal dq.

Dado que el enunciado informa que la carga de la barra es Q, positiva, el campo dE es saliente a la barra y dirigido a lo largo de la línea que une a dq con P:

El vector se ha destacado en color azul para mayor claridad. Por lo tanto, el campo estará dirigido a lo largo del eje x en sentido positivo.

Todo está listo para calcular la integral:

Recuérdese que la distancia r es la que hay entre la carga infinitesimalmente pequeña y el punto P donde se desea calcular el campo. Se ha resaltado en la figura de arriba como r= d+L-x.

Paso 5

En este paso, se integra sobre toda la distribución de carga y se resuelve la integral. Obsérvese que la variable de integración es “x” y que varía desde x=0 hasta x=L, es decir, se integra por toda la extensión de la barra. La integral dará el campo eléctrico total en el punto P:

Haciendo el cambio de variable:

u =d+L-x; du = -dx

Cuando x=0, u=d+L y cuando x=L, u = d, la se transforma en:

En ocasiones, es conveniente expresar el resultado en términos de la carga total Q presente en la barra, en vez de la densidad de carga. Entonces, sabiendo que Q=λ∙L:

Paso 6

Verificar la ecuación obtenida desde el punto de vista de las dimensiones.

La expresión para cualquier campo eléctrico, en unidades del Sistema Internacional, contiene:

• La constante electrostática k, o bien la equivalente en términos de la permitividad del vacío ε₀, sabiendo que k = 1 / (4πε₀) y ε₀ ≈ 8.854 × 10⁻¹² C²/N·m².
• Carga eléctrica en el numerador.
• Una distancia al cuadrado en el denominador.

Según esto, la ecuación que se obtuvo en el paso 5 es correcta desde el punto de vista dimensional.

Otra forma de verificar que la ecuación es correcta es hacer tender L a 0 (¿por qué?) y ver que se obtiene la expresión para el campo eléctrico producido por una carga puntual:

Resumen

Cuando se tiene una distribución de carga continua y se quiere el calcular el campo que produce en cualquier punto P, hay que:

• Establecer un sistema de referencia adecuado.
• Dividir la distribución en pequeñas cargas infinitesimales.
• Expresar el diferencial de carga en términos de la densidad de carga y la geometría de la distribución.
• Armar la integral, cuyos límites estarán dados por la geometría de la distribución y recordando que el campo eléctrico es un vector, por lo que, en principio, habrá una integral por cada componente.
• Aprovechar las simetrías, si las hay, con el fin de facilitar y simplificar los cálculos. Por ejemplo, el campo de una distribución de carga esférica debe ser radial.
• Aplicar un método para la resolución de la integral. Si la distribución carece de simetría, un método numérico siempre será de utilidad.

Por F. Zapata.

Lanzamiento de proyectil: Ejercicio resuelto

 

Densidad, porosidad y permeabilidad de las rocas

Las propiedades de las rocas dependen en gran medida de los elementos que las componen, los procesos que le dieron origen y la disposición de las partículas constituyentes, entre otras variables.

Entre las propiedades más destacadas por su importancia geofísica, se encuentran:

• Densidad
• Porosidad
• Permeabilidad

Ello se debe a que cantidad de hidrocarburos que pueden contener las rocas está determinada por los espacios disponibles entre ellas, aunado a la capacidad de los fluidos para desplazarse en el sustrato rocoso.

La piedra pómez es capaz de flotar en el agua debido a que su densidad aparente es cerca de la mitad de la del agua. Fuente: Wikimedia Commons.

Densidad y peso específico

Se define como el cociente entre la masa M y el volumen V de una roca. Por lo general, se designa con la letra griega ρ:

ρ = masa / volumen

ρ = m /V

 En el Sistema Internacional, la unidad para la densidad es kg/m³, pero suele utilizarse también g/cm³. La densidad del agua se toma como g/cm³ y sirve como patrón de referencia para las densidades de otras sustancias. Por ejemplo, una roca cuya densidad sea 2.5 g/cm³ es 2.5 veces más densa que el agua.

La densidad depende en gran medida de la composición de la roca, pero también de la disposición de los granos que la conforman. Como estos tienen formas irregulares, al agruparse normalmente dejarán pequeños espacios vacíos, lo cual influye en el valor de la densidad.

Por ejemplo, se sabe que la arena se compone de fragmentos de ciertos minerales, pero al tomar una muestra, su densidad resulta menor de lo esperado, debido a la presencia de estos poros.

Más aún, los poros o espacios podrían estar llenos de algún fluido, contribuyendo a la disminución de la densidad.

Si bien la densidad es una característica importante de las rocas, ya que no depende del tamaño de la muestra, su valor no se mantiene constante. Es sabido que se incrementa con la profundidad debido a la compactación causada la presión y también por la cementación que ocurre con el tiempo.

Alternativamente, al comparar con el volumen de la roca puede utilizarse el peso de la roca en vez de la masa. En ese caso, se habla del peso específico y se denota por la letra griega γ:

γ = peso / volumen

γ = mg /V

En el Sistema Internacional, la unidad para el peso específico es N/m³, ya que el peso es una fuerza y se mide en newton (N).

Ambas magnitudes, densidad y peso específico, están relacionadas mediante el valor de g, la aceleración de la gravedad:

γ = mg/V = ρg

Muchas veces se emplean indistintamente la densidad y el peso específico, tratándolas como si fueran la misma magnitud, pero conviene recordar que la masa está relacionada con la cantidad de materia, mientras que el peso lo está con la fuerza de gravedad. Por lo tanto, densidad y peso específico son magnitudes diferentes.

Densidad aparente

En la definición anterior, no se hizo distinción alguna entre la parte sólida o grano de la roca y los espacios vacíos. Por este motivo, a la densidad calculada de esta manera se la conoce como densidad aparente. Su valor es menor que el de la densidad del grano, es decir, el mineral constituyente.

Una forma de medir la densidad aparente de una muestra es secándola previamente, para luego pesarla. El volumen se determina con el método de la probeta (basado en el principio de Arquímedes) si se trata de rocas de baja porosidad, en caso contrario, se utiliza la picnometría o el densitómetro de gases.

Porosidad

La porosidad de una roca es la fracción del volumen de espacio entre las partículas sólidas de la roca, respecto al volumen total de la roca. El espacio incluye toda clase de cavidades (poros, grietas, fracturas) entre las partículas, así como espacios inter e intra-cristalinos:

Como puede verse, la porosidad es adimensional, por el cociente entre dos volúmenes. Ahora bien, el volumen ocupado por los poros es la diferencia entre el volumen total y el volumen de las partículas sólida de la roca, es decir, el volumen de la matriz:

Obsérvese que la porosidad no indica nada acerca de la forma de los poros ni la manera en que están distribuidos dentro de la roca, pero se puede llegar a conocer mediante experimentos de porosimetría, ya sea de manera directa o indirecta, a través de su relación con otras propiedades.

Porosidad total y porosidad efectiva

La porosidad total es la porosidad tal como se definió anteriormente: la fracción del volumen aparente ocupada por el espacio poroso total.

Por su parte, la porosidad efectiva es la fracción del volumen ocupado por el espacio poroso interconectado, que será menor que la porosidad total.

Permeabilidad

Esta magnitud mide la facilidad con la que un fluido se desplaza por los poros de la roca. Como depende no solo del tamaño de los poros, sino de lo bien interconectados que estén, la permeabilidad está relacionada con la porosidad efectiva.

La permeabilidad también se ve afectada por la compactación y la cementación, por lo que la profundidad tiende a disminuir la permeabilidad.

Matemáticamente, la permeabilidad k se determina a través de la ecuación de Darcy, la cual establece que la velocidad media u del fluido en la roca es:

• Directamente proporcional a la permeabilidad íntrinseca k y al gradiente hidráulico, siendo este la variación diferencial de la presión (proporcional a la altura en el manómetro) respecto a la dirección en que se mueve el fluido (dp/dl).

• Inversamente proporcional a la viscosidad del fluido μ:

En forma matemática, resulta así:

La unidad de la permeabilidad utilizada en la industria es el darcy, cuando el gradiente hidráulico se mide en atmósfera/centímetro y la viscosidad en centipoise. 

Tiene sentido pensar que la velocidad media sea inversamente proporcional a la viscosidad, pues un fluido muy viscoso se moverá en el medio con más lentitud que, digamos, el agua. 

También es frecuente encontrar la ecuación de Darcy en términos del caudal Q y el área de la sección transversal con A. En ese caso, llamando I al gradiente hidráulico, resulta:

Donde la constante de proporcionalidad es el coeficiente de permeabilidad K, relacionado con la permeabilidad intrínseca k mediante:

Normalmente, la permeabilidad se encuentra de manera indirecta a partir de la porosidad, la saturación de fluidos, etc., usando para ello muestras extraídas del suelo que posteriormente son analizadas en el laboratorio.

Los resultados de estos ensayos en los que se determinan los valores de la densidad, porosidad y permeabilidad, junto a otras magnitudes de interés como la resistividad, dirán si un determinado pozo petrolero es o no es de interés para la producción. 

Por F. Zapata

Tipos de rocas

Las rocas se presentan en infinidad de formas, tamaños y colores. Su estudio es 
fundamental para la búsqueda de recursos minerales y la comprensión del planeta Tierra.
Los científicos las han agrupado en tres grandes categorías que a su vez se relacionan entre sí:

 

• Ígneas
• Sedimentarias
• Metamórficas

Las rocas vienen en infinidad de características, formas y colores debido a los procesos que les dieron origen. Fuente: Pexels.

 

Rocas ígneas

Se forman por el enfriamiento y la posterior solidificación del magma, que es el material rocoso fundido que se encuentra a varios niveles de profundidad en la corteza y el manto terrestres. 

Como el proceso de enfriamiento del magma es relativamente lento bajo la superficie, se van formando cristales grandes al solidificarse, conformando las rocas intrusivas, que van quedando expuestas en la superficie a causa de la erosión.

El principal ejemplo de este tipo de roca es el granito, el constituyente principal de la corteza terrestre.

 Otras veces, el magma emerge a la superficie desde el interior de la Tierra, como ocurre durante las erupciones volcánicas. Entonces se le conoce como lava, la cual se enfría rápidamente, dando lugar a rocas formadas por cristales de menor tamaño.

Estas son las rocas extrusivas, siendo las más conocidas los basaltos, ricas en minerales como hierro y magnesio, de allí que sean más densas que los granitos.

Columnas de basalto en Rumania. Fuente: Wikimedia Commons.

 

Rocas sedimentarias

 Son las rocas formadas a partir de sedimentos acumulados en la superficie terrestre, la cual es afectada continuamente por la erosión, un proceso natural de desgaste originado por multitud de agentes como el agua, los vientos y la acción de los glaciares, entre otros.

Estos procesos desgastan la superficie, transportando partículas que luego se acumulan en forma de capas en distintos lugares. Estas capas se van litificando, es decir, se van convirtiendo en roca mediante dos procesos básicos:

• Compactación, por acción mecánica del peso que va comprimiendo los materiales poco a poco.
• 
  
• Cementación, causada por el agua que se va filtrando a través de los espacios entre los sedimentos. Con el tiempo, los materiales disueltos en el agua precipitan en esos espacios, convirtiéndose en masa sólida.

 Durante estos procesos, la composición original de la roca puede verse alterada por reacciones químicas, aunque en otras ocasiones se mantiene más o menos inalterada.

 Esto da lugar a dos tipos de rocas sedimentarias:

• Clásticas
• Químicas

Rocas sedimentarias clásticas

Las rocas sedimentarias clásticas se componen de fragmentos de índole diversa, que pueden incluir no solo minerales, sino restos de plantas y conchas marinas. Muchas de ellas son importantes por su capacidad de actuar como rocas reservorio, es decir, que pueden almacenar hidrocarburos en sus poros y fracturas.

Suelen diferenciarse por el tamaño de sus partículas, siendo las más destacadas en esta categoría las lutitas y las areniscas.

La lutita es una roca de grano fino cuyas partículas suelen tener menos de 1/256 mm, mientras que en la arenisca predominan granos similares en tamaño a la arena, entre 1/16 y 2 mm. 

Rocas sedimentarias químicas

Estas rocas se distinguen fundamentalmente por su composición química. Surgen mediante la cristalización de minerales a partir de la acción del agua en la que vienen disueltos diversos compuestos.

Sobresalen como ejemplo de estas rocas sedimentarias las calizas, que son las más comunes, y la sal de roca o halita, de gran importancia económica y cultural desde tiempos neolíticos.

Por sus características, las rocas sedimentarias químicas tienen gran importancia en la investigación del pasado terrestre, pues contienen muchísima información relevante acerca de los ambientes que les dieron origen y cómo los sedimentos llegaron hasta un determinado lugar.

Si bien las rocas sedimentarias no son las más abundantes en la Tierra, sí que son las más abundantes en su superficie, lo cual tiene sentido, puesto que se forman mediante procesos que tienen lugar a niveles muy superficiales de la Tierra.

Los acantilados blancos de Dover, Inglaterra, compuestos de caliza de Creta de origen orgánico. Fuente: tofoli.douglas a través de Flickr.

Rocas metamórficas

Las rocas metamórficas, como su nombre lo indica, se producen mediante transformaciones de las rocas ya descritas o incluso de otras rocas metamórficas. De manera que cada roca metamórfica tiene una “roca madre” que le dio origen, aunque no siempre es tarea fácil averiguar cuál fue.

Los procesos que crean rocas metamórficas están vinculados a cambios de presión y temperatura, si bien su actuación puede ser de baja intensidad (metamorfismo de grado bajo)  o de alta intensidad (metamorfismo de grado alto).

Así, un metamorfismo de grado bajo puede transformar una lutita en pizarra, que es una roca mucho más compacta. Pero un metamorfismo de grado alto puede causar una transformación mucho más radical, a tal punto que hace imposible identificar la roca madre.

Entre estos extremos de metamorfismo hay toda una gama de grados intermedios que dan lugar a gran variedad de texturas y composición química, produciendo en muchos casos una cristalización en llamativas bandas llamada foliación.

Los esquistos y los gneis son excelentes ejemplos de esta clase de rocas metamórficas.

Muestra de filita, compuesta principalmente por micas y provienente del metamorfismo de las lutitas. Fuente: Flickr.

El ciclo de las rocas

Los tres tipos de rocas descritos se conectan mediante un ciclo continuo y dinámico. Es el llamado ciclo de las rocas.

Esto significa que las características de una roca no permanecen inmutables en el tiempo. Por ejemplo, las rocas ígneas se desgastan y se convierten en sedimentos, que más tarde dan lugar a rocas sedimentarias mediante compactación y/o cementación. También pueden sufrir cambios cuando se encuentran en ambientes extremos, dando lugar a rocas metamórficas, que a su vez pueden originar sedimentos.

De igual forma, las rocas metamórficas y sedimentarias se pueden fundir para crear rocas ígneas y así sucesivamente, como ha venido ocurriendo en la Tierra desde hace millones de años, ya que este ciclo forma parte de las numerosas dinámicas que tiene el planeta para transformar y reciclar materiales. 

Distribuciones de carga continua

Se dice que los objetos de tamaño mensurable con carga eléctrica son distribuciones de carga continua. Tales distribuciones deben tener, al menos, una dimensión medible o mensurable.

Recuérdese que en post anteriores, se ha hecho referencia a las ‘cargas puntuales’, las cuales son cargas eléctricas tan, pero tan pequeñas, que no se requiere tener en cuenta sus dimensiones. Pero en el caso de las distribuciones continuas, el tamaño sí importa.

Un alambre delgado cargado eléctricamente es una distribución de carga continua. Fuente: Flickr.

La distribución de carga continua más simple es el alambre o la varilla delgada cargada eléctricamente. La carga puede distribuirse de manera equitativa a lo largo de toda la longitud, o bien puede seguir alguna distribución particular, como por ejemplo, concentrarse más en un extremo del alambre y menos en el otro, o concentrarse en el centro.

En cada caso, el campo eléctrico producido por dicha distribución será diferente, dependiendo de la ubicación de la carga y el punto donde se quiera calcular el campo. Por ejemplo, si la varilla o alambre tiene carga uniformemente distribuida, y el punto de interés se localiza en el eje del alambre, a cierta distancia de un extremo, no será igual el campo que produce allí el extremo más cercano del alambre, que el que produce el extremo más lejano, como es lógico.

El extremo más lejano produce un campo menos intenso, en razón de su lejanía, mientras que el extremo más cercano produce un campo más intenso.

La pregunta que surge es: ¿cómo tener en cuenta estas diferencias a la hora de calcular el campo eléctrico? Después de todo, la ley de Coulomb se define, en principio, para cargas puntuales, por lo tanto, ¿cómo se la puede aplicar para calcular el campo eléctrico de un objeto continuo en un punto dado?

 

Estrategia para calcular el campo eléctrico de una distribución continua

Es tan simple que se puede resumir en tres pasos:

• Se ‘divide’ (matemáticamente, claro está) el objeto en multitud de cargas minúsculas, que pueden considerarse ‘puntuales’.
• Se aplica a cada una de estas cargas la bien conocida ley de Coulomb para el campo eléctrico.
• Finalmente, se suman (vectorialmente) todos los campos eléctricos así obtenidos (¡hay que resolver una integral!) y ya se tiene por fin el campo eléctrico resultante en el punto en cuestión.

Ahora, hagamos un gráfico que ilustre lo antes dicho. Se tiene un objeto con carga eléctrica Q, distribuida sobre él, la cual, por comodidad, se supondrá positiva. El objeto tiene una forma arbitraria.

Se toma una pequeña porción del objeto, que contiene una pequeñísima porción de carga, la cual se llamará dq. Este será nuestro diferencial de carga, representado por el cubito en la parte superior del objeto en la figura de abajo.

Luego se elige un punto P en los alrededores, que dista una determinada distancia r de dq. Allí, nuestra dq produce en P una pequeña contribución del campo eléctrico dE, la cual se puede calcular a través de la ley de Coulomb para cargas puntuales:

Recuérdese que el campo eléctrico es un vector, de allí que es necesario especificar siempre su dirección, por eso se requiere escribir siempre el vector unitario respectivo. En el caso de una distribución de carga positiva, el campo es saliente, mientras que si es negativa, el campo es entrante a la misma.

Esquema de la aplicación de la ley de Coulomb para el campo eléctrico en una distribución de carga continua.

El campo eléctrico resultante en P, producido por todas las pequeñas contribuciones ubicadas en los distintos lugares del objeto, hasta cubrirlo por completo, es la integral efectuada sobre todo el volumen V del objeto.

Si el objeto no tiene un volumen apreciable, pero sí una superficie S mensurable, la integral se hará sobre dicha superficie:

Por último, si la dimensión mensurable del objeto es su longitud L, como en el caso del alambre mencionado al comienzo, la integral se llevará a cabo sobre dicha longitud.

Este es el procedimiento general para trabajar con distribuciones de carga continua, ya que cada caso tendrá su propia geometría, es decir, unos determinados dq y un r, los cuales deberán expresarse convenientemente para poder calcular la respectiva integral y obtener el campo.  

 

Densidades de carga eléctrica

El concepto de densidad de carga, análogo al ya familiar de densidad de masa, ayudará a establecer el dq apropiado para calcular la integral del campo eléctrico.

En esta imagen se resumen las tres posibilidades geométricas discutidas en el apartado anterior: distribución lineal de carga, con una densidad de carga lineal, distribución superficial de carga, con una densidad de carga superficial y, por último, la distribución de carga volumétrica, son su densidad de carga volumétrica.

Fuente: hyperphysics.

Se han elegido letras griegas para simbolizar a cada densidad de carga, como se explica seguidamente:

Densidad de carga lineal

Se representa como λ, cuyas unidades son culombios por metro (C/m)

En este caso:

→ Cálculo de la carga total

En ocasiones, es preciso calcular la carga total Q distribuida sobre el alambre.

• Si la densidad es uniforme, el cálculo es muy simple:

Q=λ∙L

• Si la densidad es no uniforme, sino que depende de alguna coordenada espacial, digamos ‘x’, entonces hay que integrar sobre dicha dimensión, tomando una longitud infinitesimal sobre el alambre, dada por dx:

Donde L representa la longitud total del alambre.

 

Densidad de carga superficial

Se representa mediante σ, cuyas unidades son culombios por metro cuadrado (C/m²)

En este caso:

     

• ‘dS’ es una superficie infinitesimal
•  σ puede ser uniforme, o bien ser una función de las coordenadas espaciales.

 

→ Cálculo de la carga total

• Si la densidad es uniforme:

Q=σ∙S

• Si la densidad es no uniforme, sino que depende de las coordenadas espaciales, digamos ‘x’ e ‘y’, entonces hay que integrar sobre la superficie S:

Donde dS representa una superficie muy pequeña del objeto (infinitesimal).

 

Densidad de carga volumétrica

Se la denota como ρ, cuyas unidades son culombios por metro cúbico (C/m³).

En este caso:

• ‘dV’ es un volumen infinitesimal
• ρ puede ser uniforme, o bien ser una función de las coordenadas espaciales.

→ Cálculo de la carga total

• Si la densidad es uniforme:

Q=ρ∙V

• Si la densidad es no uniforme, sino que depende de las coordenadas espaciales, sino que depende de las coordenadas espaciales ‘x’, ‘y’ y ‘z’, por ejemplo, entonces hay que integrar sobre el volumen V:

Ejemplo 1

Distribución superficial de carga uniforme

Se tiene un disco de 5 cm de radio, con carga eléctrica positiva distribuida de manera uniforme en su superficie a razón de 1.2 × 10^-7 C/m². ¿Cuál es la carga total Q almacenada en el disco?

Solución

Dado que la carga está distribuida de manera uniforme sobre el disco, la carga total es directamente el producto de la densidad de carga superficial y el área del disco:

El área del disco es simplemente S =πr²:

S =πr² = π × (5×10^-2 m)² = 0.0079 m²

Sabiendo que σ = 1.2 × 10^-7 C/m², la carga total guardada en el disco es:

Q=σ∙S = 1.2 × 10^-7 C/m² × 0.0079 m² = 9.5 × 10^-10 C.

Ejemplo 2

Distribución lineal de carga no uniforme

Se tiene un alambre de longitud L = 1.5 m, el cual tiene una densidad de carga dada por:

¿Cuál es la carga total en el alambre?

Solución

La carga no está distribuida uniformemente, sino que depende de la ubicación ‘x’ de cada punto sobre el alambre. Si colocamos un sistema de referencia donde el alambre se ubica sobre el eje horizontal (el eje x), y los tonos de gris representan la carga, en x=0 será blanco (porque no hay carga) mientras que en x = 1.5 m la densidad de carga será máxima, por eso se ve en negro.

Un segmento arbitrario dx, que contiene una pequeña carga dq, ubicado en un lugar arbitrario del alambre, tendrá una densidad de carga intermedia. La figura servirá luego para calcular el campo eléctrico del alambre, pero eso queda para otro post.

Ahora vamos al cálculo de la carga total, que es muy simple:

Por F. Zapata.