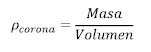Las propiedades de las rocas dependen en gran medida de los elementos que las componen, los procesos que le dieron origen y la disposición de las partículas constituyentes, entre otras variables.
Entre las propiedades más destacadas por su importancia geofísica, se encuentran:
- Densidad
- Porosidad
- Permeabilidad
Ello se debe a que cantidad de
hidrocarburos que pueden contener las rocas está determinada por los espacios
disponibles entre ellas, aunado a la capacidad de los fluidos para desplazarse
en el sustrato rocoso.
 |
| La piedra pómez es capaz de flotar en el agua debido a que su densidad aparente es cerca de la mitad de la del agua. Fuente: Wikimedia Commons. |
Densidad y peso específico
Se define como el cociente entre la masa M y el volumen V de una roca. Por lo general, se designa con la letra griega ρ:
ρ = masa / volumen
ρ = m /V
En el Sistema Internacional, la unidad para la densidad es kg/m3, pero suele utilizarse también g/cm3. La densidad del agua se toma como g/cm3 y sirve como patrón de referencia para las densidades de otras sustancias. Por ejemplo, una roca cuya densidad sea 2.5 g/cm3 es 2.5 veces más densa que el agua.
La densidad depende en gran medida de la
composición de la roca, pero también de la disposición de los granos que la
conforman. Como estos tienen formas irregulares, al agruparse normalmente
dejarán pequeños espacios vacíos, lo cual influye en el valor de la densidad.
Por ejemplo, se
sabe que la arena se compone de fragmentos de ciertos minerales, pero al tomar
una muestra, su densidad resulta menor de lo esperado, debido a la presencia de
estos poros.
Más aún, los poros
o espacios podrían estar llenos de algún fluido, contribuyendo a la disminución
de la densidad.
Si bien la densidad es una característica importante
de las rocas, ya que no depende del tamaño de la muestra, su valor no se
mantiene constante. Es sabido que se incrementa con la profundidad debido a la
compactación causada la presión y también por la cementación que ocurre con el
tiempo.
Alternativamente, al comparar con el
volumen de la roca puede utilizarse el peso de la roca en vez de la
masa. En ese caso, se habla del peso específico y se denota por la letra
griega γ:
γ = peso / volumen
γ = mg /V
En el Sistema Internacional, la unidad para el peso específico es N/m3, ya que el peso es una fuerza y se mide en newton (N).
Ambas magnitudes, densidad y peso específico,
están relacionadas mediante el valor de g, la aceleración de la gravedad:
γ = mg/V = ρg
Muchas veces se emplean indistintamente la densidad y el peso específico, tratándolas como si fueran la misma magnitud, pero conviene recordar que la masa está relacionada con la cantidad de materia, mientras que el peso lo está con la fuerza de gravedad. Por lo tanto, densidad y peso específico son magnitudes diferentes.
Densidad aparente
En la definición anterior, no se hizo
distinción alguna entre la parte sólida o grano de la roca y los espacios
vacíos. Por este motivo, a la densidad calculada de esta manera se la conoce
como densidad aparente. Su valor es menor que el de la densidad del
grano, es decir, el mineral constituyente.
Una forma de medir la densidad aparente de una muestra es secándola previamente, para luego pesarla. El volumen se determina con el método de la probeta (basado en el principio de Arquímedes) si se trata de rocas de baja porosidad, en caso contrario, se utiliza la picnometría o el densitómetro de gases.
Porosidad
La porosidad de una roca es la fracción del volumen de espacio entre las partículas sólidas de la roca, respecto al volumen total de la roca. El espacio incluye toda clase de cavidades (poros, grietas, fracturas) entre las partículas, así como espacios inter e intra-cristalinos:Como puede verse, la porosidad es
adimensional, por el cociente entre dos volúmenes. Ahora bien, el volumen ocupado
por los poros es la diferencia entre el volumen total y el volumen de las partículas
sólida de la roca, es decir, el volumen de la matriz:
Obsérvese que la porosidad no indica nada
acerca de la forma de los poros ni la manera en que están distribuidos dentro
de la roca, pero se puede llegar a conocer mediante experimentos de porosimetría,
ya sea de manera directa o indirecta, a través de su relación con otras
propiedades.
Porosidad total y porosidad efectiva
La porosidad total es la porosidad
tal como se definió anteriormente: la fracción del volumen aparente ocupada por
el espacio poroso total.
Por su parte, la porosidad efectiva
es la fracción del volumen ocupado por el espacio poroso interconectado,
que será menor que la porosidad total.
Permeabilidad
Esta magnitud mide la facilidad con la
que un fluido se desplaza por los poros de la roca. Como depende no solo del
tamaño de los poros, sino de lo bien interconectados que estén, la
permeabilidad está relacionada con la porosidad efectiva.
La permeabilidad también se ve afectada
por la compactación y la cementación, por lo que la profundidad tiende a
disminuir la permeabilidad.
Matemáticamente, la permeabilidad k se determina a través de la ecuación de Darcy, la cual establece que la velocidad media u del fluido en la roca es:
- Directamente proporcional a la permeabilidad íntrinseca k y al gradiente hidráulico, siendo este la variación diferencial de la presión (proporcional a la altura en el manómetro) respecto a la dirección en que se mueve el fluido (dp/dl).
- Inversamente proporcional a la viscosidad del fluido μ:
La unidad de la permeabilidad utilizada en la industria es el darcy, cuando el gradiente hidráulico se mide en atmósfera/centímetro y la viscosidad en centipoise.
Tiene sentido pensar que la velocidad media sea inversamente proporcional a la viscosidad, pues un fluido muy viscoso se moverá en el medio con más lentitud que, digamos, el agua.
También es frecuente encontrar la ecuación de Darcy en términos del caudal Q y el área de la sección transversal con A. En ese caso, llamando I al gradiente hidráulico, resulta:
Normalmente, la permeabilidad se
encuentra de manera indirecta a partir de la porosidad, la saturación de
fluidos, etc., usando para ello muestras extraídas del suelo que posteriormente
son analizadas en el laboratorio.
Los resultados de estos ensayos en los que se determinan los valores de la densidad, porosidad y permeabilidad, junto a otras magnitudes de interés como la resistividad, dirán si
un determinado pozo petrolero es o no es de interés para la producción.
Por F. Zapata