Los vectores en tres dimensiones o vectores en el espacio, requieren
tres coordenadas para ser representados, y hay varias notaciones disponibles,
como hemos visto en posts anteriores. Por ejemplo, se pueden denotar como:
v = < vx, vy, vz >
v = vx i + vy j
+ vz k
 |
| Vector en tres dimensiones. Fuente: F. Zapata. |
Donde vx, vy y vz representan las coordenadas cartesianas del vector v, el cual se escribe con letra negrita en texto impreso, o bien con una flechita encima, también en texto impreso o manuscrito, así:
Para representar un vector en el espacio, se hace uso de un sistema de coordenadas cartesianas, al igual que con los vectores en el plano. En la figura de arriba se tiene un vector v, cuyas componentes cartesianas son x1, y1 y z1. Las componentes x1, y1 yacen sobre el plano xy, el cual podría representar el suelo, por ejemplo. Entonces la componente z1 es vertical.
La magnitud del vector, que no es más
que su módulo, se representa sin flecha encima en texto manuscrito, o sin
negritas en texto impreso, y se calcula mediante:
Cosenos
directores
En la siguiente imagen se muestra el
vector v, que forma un ángulo con cada uno de los ejes coordenados. El
ángulo α es el ángulo entre v y el eje
x, el ángulo β es el que se forma entre v y el eje y, y por último, el ángulo γ se forma entre v y el eje z.
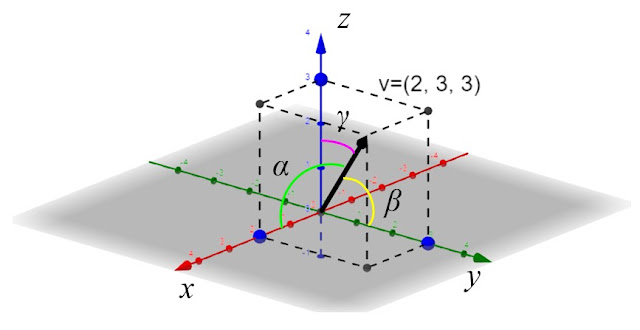 |
| Cosenos directores. Fuente: Geogebra. Mod. por F. Zapata. |
Si se conocen estos tres ángulos, se tiene la dirección del vector v, y su medida se calcula muy fácilmente, a través de la proyección del vector v sobre cada uno de los ejes coordenados, que no es otra cosa que la respectiva componente del vector. Así:
- · vx = v ∙ cos α (2)
- · vy = v ∙ cos β
- · vz = v ∙ cos γ
Los cosenos de cada uno de estos
ángulos reciben el nombre de cosenos directores. Puede formarse un
vector unitario en la dirección de v con los cosenos directores,
partiendo de la definición de vector unitario:
(3)
Puesto que la magnitud de cualquier vector unitario es 1, entonces una importante propiedad de los cosenos directores es:
Ejemplo
1
Calcular los cosenos directores del
vector v mostrado en la figura de arriba y la medida de α, β y γ.
Además, calcular el vector unitario en la dirección de v.
Solución
En primer lugar se calcula la
magnitud del vector mediante (1):
Las componentes de v son: vx
= 2; vy = 3; vz = 3, por lo tanto, de acuerdo a (2):
Y el vector unitario u en la
dirección de v es, según la ecuación (4):
u = 0.4264 i + 0.6396 j + 0.6396 k
Ejemplo
2
En la siguiente figura, la línea que une al extremo de la fuerza F con el punto A es paralela al eje y, y dicho punto A se encuentra en el plano xz, además, se sabe que la componente Fx vale 100 N. Determinar:
a) La magnitud de F
b) Las componentes de F
c) Los ángulos α, β y γ que forma F con los ejes coordenados.
 |
| Fuente: Estática. Bedford. |
Solución a
Del diagrama se conoce el ángulo de
proyección de F con el plano xz, cuya medida es 20º y también el
ángulo que esta proyección forma con el eje y, de medida igual a 60º. La
proyección de F sobre el plano xz es F ∙ cos20º, y la proyección de esta, sobre el eje x, es Fx,
cuyo valor es conocido según el enunciado, siendo de 100 N, por lo tanto:
Fx = (F ∙
cos20º)∙cos 30º = 100 N
La magnitud de F es, pues:
F = 100 / (cos 20º ∙ cos 30º) N = 122.88 N
Solución b
De la figura se ve que el ángulo β que forma el vector F con el eje y es 70º. Entonces:
Fy = 122.88 ∙ cos 70º N = 42.03 N
Ahora bien:
Fz = (F ∙
cos20º)∙cos 60º = (122.88∙ cos20º)∙cos 60º N = 57.73 N
Y la componente Fx ya es
conocida por el enunciado, entonces:
Fx = 100 N ; Fy = 42.03 N ; Fz = 57.73 N
¿Y cómo se dibuja un vector en 4 dimensiones o más?
ResponderEliminar