Lanzamiento vertical, ecuaciones y ejemplos resueltos

El lanzamiento vertical consiste en un movimiento de aceleración constante bajo la acción de la gravedad. El móvil puede estar subiendo o bajando en un momento dado, pero para subir, necesita que se le proporcione una velocidad inicial v_o.
Gracias a la velocidad inicial el móvil asciende, alcanza una cierta altura máxima, que depende de esta velocidad inicial, y luego inicia el descenso hasta llegar a la superficie. Sin importar en qué fase del movimiento se encuentre, la aceleración siempre es g = 9.8 m/s² y está dirigida verticalmente hacia abajo.

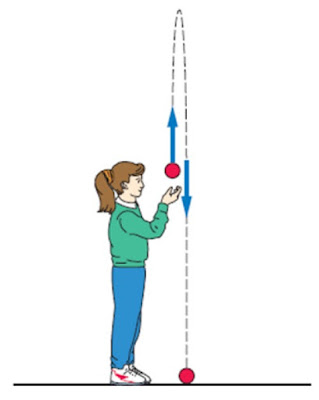Figura 1. Una niña lanza verticalmente hacia arriba una pelota. Fuente:
Thomas Griffith, W. 2007. Física Conceptual. Mc Graw Hill.

También se le puede proporcionar al móvil una velocidad inicial hacia abajo, que la gravedad se ocupa de impulsar, agregando cada vez más velocidad al objeto hasta que este logra llegar a la superficie.

Ecuaciones del lanzamiento vertical

Son las mismas que las del movimiento rectilíneo uniformemente acelerado, en las cuales tomaremos al eje y, el eje vertical, como la dirección del movimiento. Además daremos el sentido positivo hacia arriba y el negativo hacia abajo.

Con esta elección la gravedad se toma como -9.8 m/s², el signo ya indica que está dirigida hacia abajo:

-Posición en función del tiempo: y (t) = y_o + v_o t  - ½gt²
-Velocidad en función del tiempo: v (t) = v_o – gt
-Velocidad en función de la posición: v² =v_o² - 2.g.Dy

Donde yo es la posición inicial del movimiento, que siempre se recomienda escoger en el punto de lanzamiento y hacerla 0, para simplificar las ecuaciones.

Nótese que en el lanzamiento vertical la velocidad inicial v_o siempre es diferente de 0, aún cuando el lanzamiento se efectúe hace abajo. Evidentemente que si al objeto se le proporciona una velocidad inicial, llegará al piso con  más rapidez que si se lo deja caer.

Los signos de la velocidad

Observando con cuidado las figuras 1 y 2, vemos que en un lanzamiento vertical hacia arriba, la velocidad cambia de sentido. También lo vemos en la figura 2.

Cuando la pelota sale de la mano del lanzador, la velocidad es positiva (recuerde que se asigno signo + al eje y hacia arriba). La pelota asciende, pero va perdiendo velocidad, llega a una cierta altura, se detiene momentáneamente y allí cambia el sentido de la velocidad, siendo entonces negativa cuando la pelota viene bajando.

Figura 2. Lanzamiento vertical hacia arriba, observe el cambio de signos de la velocidad. A la derecha, la gráfica de la velocidad en función del tiempo, note que la pendiente es negativa.
Fuente: Thomas Griffith, W. 2007. Física Conceptual. Mc Graw Hill.

En conclusión, el signo de la velocidad nos indica si la pelota se está moviendo hacia arriba o hacia abajo. Velocidades positivas significan que el móvil va de subida, y velocidades negativas que el móvil va bajando.

En la siguiente figura tenemos el gráfico de la velocidad en función del tiempo para un móvil que ha sido lanzado verticalmente hacia arriba desde cierta posición, con velocidad inicial de 20 m/s. La velocidad se hace 0 cuando t = 2 segundos, lo que significa que en ese tiempo alcanzó la altura máxima, que de acuerdo a la figura es de 20 m. Luego la velocidad se hace negativa, mientras el objeto desciende.

Justo cuando regresa al nivel desde donde fue lanzada la pelota, al cabo de 4 segundos, su velocidad es de -20 m/s, es decir, el objeto regresa al mismo nivel de lanzamiento con una velocidad de la misma magnitud y dirección que la velocidad inicial, pero con sentido contrario.

Aprendamos más acerca de la altura que alcanza la pelota y el tiempo que dura en el aire en las siguientes secciones.

  

La altura máxima en el lanzamiento vertical

Veamos como calcular la altura máxima que alcanza la pelota. Esta va a depender de la velocidad inicial que se le confiera: a mayor velocidad, más alto subirá. Vamos a suponer que el punto de partida del proyectil se escoge como y_o = 0 en la ecuación que vincula la velocidad con la posición:

v² =v_o² - 2.g.Dy

Como Dy = y – y_o quedaría simplemente Dy = y. En tal caso:

v² =v_o² - 2.g.y

Si el móvil se detiene momentáneamente al alcanzar la altura máxima, llamada y_máx, entonces tendremos v = 0 y con eso:

0 =v_o² - 2.g.y_máx

Por lo tanto:

y_máx = v_o²/2g

En efecto, podemos ver que la altura máxima depende del cuadrado de la velocidad inicial.

El tiempo máximo y el tiempo de vuelo

El tiempo máximo, denotado t_máx,  es el tiempo que tarda el objeto lanzado verticalmente hacia arriba en alcanzar su altura máxima. Depende de la velocidad inicial que se le confiera al objeto. Como sabemos que allí se detiene momentáneamente antes de cambiar el sentido de la velocidad, hacemos v = 0 en la ecuación para la velocidad:

v (t) = v_o – gt_máx → 0 = v_o – gt_máx

Por lo tanto:

t_máx = v_o / g

Se advierte que también depende de la velocidad inicial, más no de su cuadrado, como en el caso de la altura máxima.

El tiempo de vuelo es el tiempo que dura el proyectil en el aire. Supongamos un lanzamiento vertical hacia arriba a nivel, es decir, el objeto parte de cierto punto y regresa a él.

Entonces el tiempo de vuelo es simplemente el doble del tiempo máximo. Pero si el objeto es lanzado desde cierta altura hacia arriba y en su descenso sigue de largo, como en la figura 2, entonces el tiempo de vuelo es mayor que 2t_máx y tendremos que calcularlo mediante alguna de las ecuaciones dadas arriba, según los datos que ofrezca el problema.

Ejemplos resueltos

Ejemplo resuelto 1

Se lanza una pelota verticalmente hacia arriba con una rapidez inicial de 26.4 m/s. ¿Cuánto tarda en regresar al punto de partida?

Solución

Calculamos el tiempo máximo y lo multiplicamos por 2:

t_máx = v_o / g =  26.4 m/s / 9.8 m/s² = 2.69 s

2. t_máx = 2. 2.69 s = 5.39 s.

Ejemplo resuelto 2

Se lanza una piedra hacia arriba, desde el nivel del suelo, con una velocidad inicial de 10.0 m/s.

a) ¿Cuál es la velocidad de la piedra después de 0.50 s?

b) ¿A qué altura sobre el nivel del suelo está la piedra después de 0.50 s?

Solución a

v(t) = v_o – gt

v(0.5) = 10.0  – 9.8 x 0.5 m/s = 5.1 m/s

Solución b

Tomaremos y_o = 0

y(t) = v_o t  - ½gt²

Por lo tanto:

y(0.5) = 10.0 x 0.5  - ½ x 9.5 x 0.5² m = 3.8 m

Ejemplo resuelto 3

Se lanza una piedra hacia abajo con una velocidad inicial de 10.0 m/s. La aceleración de la piedra es constante y tiene el valor de la aceleración en caída libre, 9.81 m/s². ¿Cuál es la velocidad de la piedra después de 0.500 s?

v(t) = v_o – gt = -10.0 – 9.81 x 0. 500 m/s = -14.905 m/s

Por F. Zapata

Referencias

1. Bauer, W. 2011. Física para Ingeniería y Ciencias. Volumen 1. Mc Graw Hill.
2. Thomas Griffith, W. 2007. Física Conceptual. Mc Graw Hill.