 |
| El límite mostrado en la imagen es un límite notable mediante el cual se define el número ‘e’, de innumerables aplicaciones en ciencia. |
Ejercicio 1
Límite por sustitución directa
Calcular, si es que existe, el siguiente
límite:
Solución
Ejercicio 2
Límite por sustitución directa
Solución
Ejercicio 3
Límite usando tabla de valores
Solución
Si el límite existe,
pronto se hará evidente al examinar los resultados:
En este caso, el límite buscado vale 2, pues los resultados muestran que la función se acerca cada vez más a este valor, cuando x se acerca más y más 1.
Ejercicio 4
Límite usando tabla de valores
La tendencia en los valores es acercarse
cada vez más a f(x) = ─1, por lo tanto:
Ejercicio 5
Límite a través de gráficas
Calcular, si existe, el siguiente límite
mediante la inspección de la gráfica:
Solución
Examinando la gráfica, se concluye que el
límite de la función cuando x tiende a -2 no existe. En efecto, al acercarse a
x=2 desde la izquierda, la función decrece rápidamente, mientras que al
acercarse desde la derecha, la función crece indefinidamente.
La recta x= −2 es una asíntota vertical de
la función.
Ejercicio 6
Límite a través de gráficas
Calcular, si existe, el siguiente límite mediante la inspección de la gráfica:
Solución
El límite de la función cuando x tiende a
-2 no existe, ya que acercándose arbitrariamente desde la izquierda a dicho
valor, la función crece indefinidamente, mientras que acercándose por la
derecha, decrece. La función tiene una asíntota vertical en dicho valor.
Solución
Se trata de un límite de la forma 0/0,
entonces se factoriza el denominador, buscando eliminar la indeterminación. El
denominador es una diferencia de cuadrados, por la tanto se escribe como el
producto de una suma por su diferencia:
Ejercicio 8
Límite mediante factorización
Calcular, si existe, el siguiente límite:
Solución
Ejercicio 9
Límite mediante racionalización
Calcular, en caso de que exista, el
siguiente límite:
Solución
Ejercicio 10
Límite mediante el uso de límites notables
Calcula el siguiente límite, mediante el uso de alguno de los límites notables:
Solución
La idea es utilizar el límite notable:















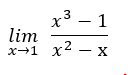







ME HA PARECIDO, MUY ENTENDIBLE SUS METODOS DE FACTORIZACIÒN, PARA QUE X . NO SE HICIERA CERO, MUCHAS GRACIAS.
ResponderEliminarMUY BIEN MAESTRO m
EliminarMonico,, ME DICE QE usted es de Navojoa, Sonora, felicidades muy inteligente