Ley de Coulomb para cargas puntuales: 6 ejercicios resueltos con solución detallada

 

Ejercicio 1 

Cargas eléctricas

La electricidad estática común involucra cargas que oscilan entre nano culombios y micro culombios. Determinar

a) La cantidad de electrones necesarios para formar una carga de −2,00 nC

b) ¿Cuántos electrones se deben eliminar de un objeto neutro para dejar una carga neta de 0,500 μC?

 

Solución a

Sabiendo que la carga eléctrica de un electrón tiene carga de −1.6×10⁻¹⁹ C, y que 1 nC=1 ×1 0⁻⁹ C, se tiene que:

−2,00 nC = −2 ×1 0⁻⁹ C

Solución b

Se tiene la siguiente equivalencia:

1 μC=1 ×1 0⁻⁶ C

Por lo tanto:

0.5 μC=0.5 ×1 0⁻⁶ C

Entonces:

Ejercicio 2 

Cargas eléctricas en una dimensión

Dos cargas de igual magnitud y de distinto signo se encuentran en el vacío, separadas una distancia de 50 centímetros. Se sabe que la magnitud de la fuerza eléctrica de atracción entre ellas es 0,9 N. ¿Cuál es la magnitud de las cargas?

Solución 

La magnitud de la fuerza de atracción entre las cargas es:

Donde q₁ y q₂ son las magnitudes de las cargas, k es la constante electrostática 9×10⁹  N•m²/C² y r la separación entre las cargas. Como las cargas tienen igual magnitud:

q₁ = q₂= Q

Reemplazando esta condición y despejando Q en la ley de Coulomb, se obtiene:

Ejercicio 3

Cargas puntuales en equilibrio electrostático

 

Sobre una línea recta se disponen tres partículas cargadas separadas por una distancia d, como se muestra en la figura. Las cargas q₁ y q₂, de distinta magnitud y signos opuestos, se mantienen fijas, mientras que una tercera carga positiva q₃ puede moverse libremente sobre la línea que las une.

¿Dónde se debe ubicar q₃  para que permanezca en equilibrio electrostático, suponiendo que la magnitud de q₂ es mayor que la de q₁?

Solución 

Sea F₁₃ la fuerza que ejerce la carga q₁ sobre la carga q₃. Al ser del mismo signo, dicha fuerza es de repulsión, en cambio, la fuerza F₂₃ es de atracción, por ser q₂ y q₃ de distinto signo. Para que q₃ se encuentre en equilibrio, la magnitud de dichas fuerzas debe ser la misma.

Para que la carga q₃ permanezca en equilibrio estático, debe colocarse a la izquierda de q₁, a cierta distancia x, ya que la magnitud de q₁ es menor que la de q₂.

Nótese que si se colocara a q₃ en medio de las otras dos cargas, la fuerza resultante estaría dirigida de izquierda a derecha, por lo que sería imposible lograr que quedara en equilibrio estático, mientras que si q₃ se colocara a la derecha de q₂, por ser esta de mayor magnitud, la fuerza F₁₃ no tendría forma de equilibrarla.

Ejercicio 4 

Cargas puntuales en equilibrio electrostático

Para el sistema de tres cargas puntuales del ejercicio 3, determinar una expresión para el valor de x, la distancia a la cual se debe colocar la carga q₃ de la carga q₁ para que se encuentre en equilibrio estático.

Solución

Partiendo de:

Se tiene que:

Por lo tanto, para que las cargas se encuentren en equilibrio electrostático, debe cumplirse que la fuerza neta se anule. Como ambas fuerzas tienen la misma dirección y sentidos opuestos, se puede prescindir de la notación vectorial e igualar sus magnitudes:

Esta es una ecuación de segundo grado, que se resuelve mediante la fórmula cuadrática:

Con:

a= q₁— q₂

b= 2dq₁

c= q₁d²

Enseguida, se sustituye cuidadosamente los términos anteriores en la ecuación cuadrática, teniendo presente que la incógnita siempre es “x”. Es importante destacar que la ecuación cuadrática tiene al menos dos soluciones, pero en este caso, se escogerá la que tenga el signo + como resultado, ya que una distancia siempre es positiva.

Ejercicio 5 

Cargas puntuales en equilibrio electrostático en dos dimensiones

Las cargas puntuales q₁ = +0.2μC ; q₂ = −0.4μC y q₃ = -0.1μC se disponen según el triángulo de la figura. Calcular la fuerza resultante sobre la carga q₁.

Solución

Se dibuja el diagrama de cuerpo libre sobre la carga q₁, seleccionando un sistema de coordenadas cartesianas adecuado:

F₁₂ (rojo) es la fuerza de atracción entre q₁ y q₂, F₁₃ (verde), es la fuerza de atracción entre q₁ y q₃. El diagrama no está necesariamente a escala.

La fuerza neta sobre q₁  es:

F_neta = F₁₂ + F₁₃

De acuerdo al sistema de referencia seleccionado, la fuerza F₁₂ tiene componentes:

F_12x = F₁₂∙senθ = F₁₂∙(4/5)= 0.8F₁₂

F_12y = F₁₂∙cosθ = F₁₂∙(3/5)= −0.6F₁₂

Por su parte, la fuerza F₁₃ está verticalmente dirigida hacia abajo, entonces:

F_neta = F₁₂ + F₁₃ = 0.8F₁₂ i + (−0.6F₁₂ − F₁₃) j

Nótese la distinción entre vectores (en negrita) y sus magnitudes. Ahora estas se pueden calcular con la ley de Coulomb:

F_neta = F₁₂ + F₁₃ = 0.8×8.64×10⁻⁵ i + (−0.6×8.64×10⁻⁵ − 2.00×10⁻⁵) j = (−6.9 i − 7.2 j) ×10⁻⁵ N

Ejercicio 6

Fuerza eléctrica entre cargas puntuales y segunda ley de Newton

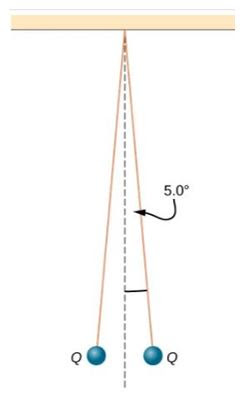
Dos bolitas, cada una de 5,0 g de masa, están atadas a hilos de seda de 50 cm de longitud, que a su vez están atados al mismo punto del techo, como se muestra en la figura. Cuando las bolitas tienen la misma carga Q, los hilos cuelgan a 5,0° respecto a la vertical, como se muestra en la figura. Determinar:

a)    La magnitud de Q

b) ¿Qué puede decirse de los signos de las dos cargas?

Solución a

En primer lugar, se dibuja un diagrama de cuerpo libre de una de las bolitas, con el fin de aplicar la segunda ley de Newton. Las bolitas se encuentran en equilibrio estático.

Tres fuerzas actúan sobre cualquiera de las bolitas:

• La tensión en la cuerda T, que forma un ángulo de 5º con la vertical.
• La fuerza de repulsión electrostática F_e
• El peso W

Ya que la tensión T está inclinada respecto al eje y, tiene dos componentes, una vertical, llamada T_y, y otra horizontal T_x, en consecuencia, al aplicar la segunda ley de Newton, se obtiene:

∑ F_y =T_y – W = 0

∑ F_x =F_e – T_x = 0

De la primera ecuación:

T_y = W ⇨ T∙cos 5º = mg

Y de la segunda:

F_e – T_x = 0 ⇨ F_e = T∙sen 5º

Por lo tanto:

La ley de Coulomb afirma que:

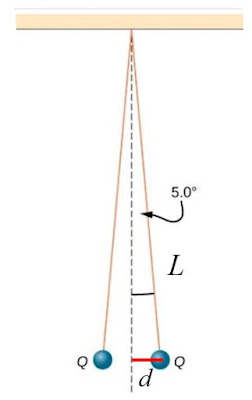
Siendo q₁ y q₂ las magnitudes de las cargas, k la constante electrostática 9×10⁹  N•m²/C² y r la separación entre las cargas. Del esquema es fácil verificar, mediante trigonometría elemental, que la distancia entre las cargas es:

r = 2d = 2L∙sen 5º

Donde L es la longitud de la cuerda, igual a 50 cm o 0.5 m.

Como las bolitas son idénticas, q₁ = q₂= Q. Al sustituir en la expresión antes deducida para F_e, resulta:

Importante: Antes de sustituir valores numéricos, es necesario asegurarse de que todas las cantidades, tales como longitudes, masas, etc., se encuentren en unidades del Sistema Internacional.

Solución b

Con la información suministrada no es posible determinar si ambas cargas son positivas o negativas, lo que sí es seguro es que son del mismo signo.

Por F. Zapata

¿Tienes dudas o necesitas más ejemplos resueltos? 

¡Podemos ayudarte! 

Déjanos un mensaje y te responderemos a la brevedad. Te brindamos asesorías personalizadas por WhatsApp y Telegram a precios solidarios:

 +058 412 7110460 

Aceptamos Paypal, Payoneer y transferencia bancaria (en este último caso solo bancos de Venezuela y Argentina).