 |
| Encuentra el límite al infinito en esta pizarra con múltiples fórmulas y ecuaciones matemáticas. Fuente: Arkansas University. |
Donde P(x) y Q(x) son polinomios de grado n
y grado m respectivamente:

Al hacer tender la variable a +∞ o a —∞, se presentan las siguientes posibilidades, cuyo resultado depende de la comparación entre los grados del numerador y del numerador:
- Cuando el grado de P(x) es menor que el grado de Q(x), la función tiende a 0 cuando x toma valores muy grandes, ya que el denominador crece más deprisa que el numerador.
- Si el grado del numerador P(x) es igual al grado del denominador Q(x), el resultado es el cociente de los coeficientes de la potencia correspondiente a n.
- Por último, si el grado del numerador es mayor que el grado al denominador, el cociente entre ambos tiene un grado mayor que 1 y en consecuencia, el límite no existe.
- Arriba a la izquierda, la función tiende al valor y= k cuando x tiende a infinito.
- A la derecha, cuando x se hace muy grande y positivo, la función crece sin medida, es decir, y tiende a + ∞.
- Abajo, a la izquierda, la función decrece sin medida cuando x tiende a infinito, es decir, es decir, y tiende a -∞.
- Por último, en la figura de la derecha, la función oscila y el límite cuando x tiende a infinito no existe.
Ejemplo 1
Calcula, de ser posible, el siguiente límite:
Solución
En primer lugar, hay que asegurarse de que el
límite corresponde a una indeterminación ∞/∞, lo cual es muy sencillo. Basta con verificar que, cuando la
variable crece, lo hace también el numerador, así como el denominador.
Una vez que
se está convencido de ello, se examina el grado del numerador y el del
denominador. En el ejemplo propuesto, ambos tienen grado 2, ya que son
polinomios cuadráticos. Al ser n=m=2, solo es necesario tener en cuenta los
términos cuadráticos, pues los términos de menor exponente se pueden despreciar
frente a estos:
Ejemplo 2
Calcula, si existe, el siguiente límite:
Solución

En este ejemplo, el denominador no es polinomio. Sin embargo, el argumento de la raíz cuadrada es un polinomio y el procedimiento anterior de eliminar los términos de grado menor puede llevarse a cabo sin mayor inconveniente:
Recuerda que puedes verificar estos límites muy fácilmente, construyendo la gráfica de la función mediante alguna herramienta online como GeoGebra o Desmos.
Ejemplo 4
Calcula el límite en caso de que exista:
Por F. Zapata

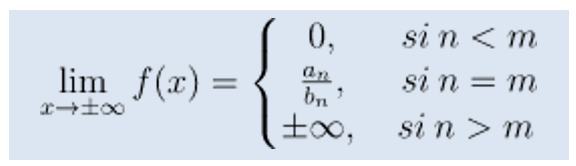






No hay comentarios:
Publicar un comentario