Asíntotas horizontales de una función

Las asíntotas horizontales son rectas horizontales que limitan el crecimiento o decrecimiento de la gráfica de una función. A diferencia de las asíntotas verticales, es posible que la función cruce a la asíntota horizontal.

En la gráfica lucen de esta manera:

Figura 1. Asíntotas horizontales de una función. Fuente: F. Zapata.

Figura 2. Una oscilación amortiguada exhibe un comportamiento asintótico. Fuente: F. Zapata.

En la gráfica es fácil advertir que cuando x se hace infinitamente grande o infinitamente pequeño, la función tiende a cierto valor f(x) = L. Por lo tanto, las asíntotas horizontales tienen la forma:

y = L

Donde L es un determinado valor real.

De acuerdo a lo antes dicho, de que x se debe hacer muy o muy pequeño para encontrar el valor de L, es inmediato afirmar que la asíntota horizontal no es otra cosa que el límite de f(x) cuando x → ∞ o cuando x → − ∞:

Si alguno de estos límites existe y vale L, ahí está la asíntota buscada, en la forma de la recta y = L.

Ahora bien, las asíntotas horizontales aparecen en funciones racionales de la forma:

Donde P(x) y Q(x) son polinomios de x. Se pueden presentar los casos siguientes:

Caso 1

El numerador es del mismo grado que el denominador, en tal caso se calcula el cociente entre los coeficientes de los respectivos grados mayores, del numerador y el denominador. La asíntota horizontal es la recta dada por el resultado del cociente.

Caso 2

El numerador tiene grado menor que el denominador, entonces la asíntota horizontal de la función es la recta:

y = 0

O lo que es igual: el eje x.

Caso 3

El numerador tiene grado mayor que el denominador, en ese caso la función no tiene asíntota horizontal.

Ejercicios resueltos

Ejercicio 1

Hallar, si existen, las asíntotas horizontales de la función:

Lo primero que hay que hacer es examinar los grados del numerador y el denominador. El polinomio P(x) = x − 1 tiene grado 1, y el polinomio Q(x) = x − 2 también, por lo que el cociente entre los coeficientes es 1.

La asíntota horizontal es la recta y = 1.

Este resultado se comprueba calculando los límites al infinito de f(x):

 

Por lo tanto, simplemente hay una sola asíntota horizontal dada por la recta y = 1. La gráfica de la función, hecha con Geogebra, lo confirma:

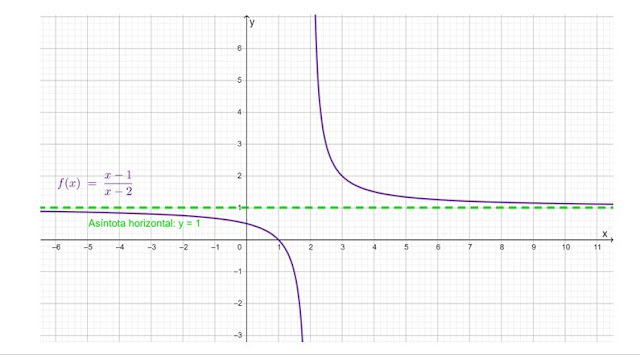Figura 3. Gráfica de f(x) mostrando la asíntota horizontal en y = 1. Fuente: F. Zapata a través de Geogebra.

En el post anterior acerca de las asíntotas verticales se había usado esta función como ejemplo, ya que posee asíntota vertical en x = 2. Y es que una función  puede tener distintos tipos de asíntotas sin ningún problema.

A continuación está el gráfico de la misma función, mostrando la asíntota horizontal y la asíntota vertical:

Figura 4.- Asíntotas horizontales y verticales de la función f(x). Fuente: F. Zapata a través de Geogebra.

Ejercicio 2 

Hallar las asíntotas horizontales y verticales de la función: 

 Solución

Para hallar las asíntotas horizontales se examinan los grados del numerador y del denominador. El polinomio P(x) = 8 es de grado 0, mientras que el polinomio Q(x) = x²+x+1 es de grado 2, el cociente 0/2 = 0, por lo tanto la asíntota horizontal es la recta y = 0.

En cuanto a las asíntotas verticales, estas serían los ceros del denominador, si los hay:

x² + x + 1 = 0

Pero esta ecuación de segundo grado no tiene raíces reales, por lo tanto la función no tiene asíntotas verticales. La gráfica hecha con Geogebra permite verificarlo:

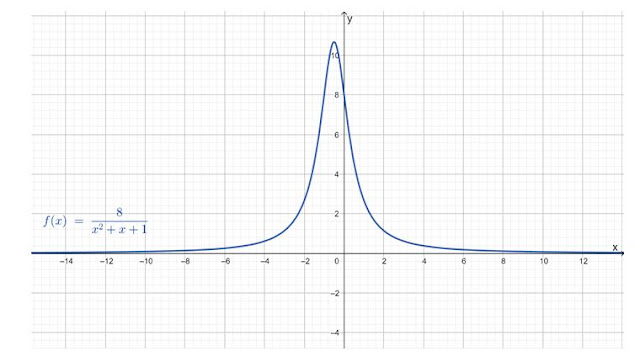Figura 5.- Gráfica de la función f(x) del ejercicio resuelto 2, en la cual el eje x es una asíntota horizontal. Fuente: F. Zapata a través de Geogebra.