El movimiento rectilíneo uniforme es aquel en el cual la velocidad media y la velocidad instantánea son iguales, por lo tanto, recorre distancias iguales en tiempos iguales, por ejemplo, si al cabo de 1 s el móvil recorre 3m, al cabo de 2s recorrerá 6m, al cabo de 3s recorrerá 9m y así sucesivamente.
Es el movimiento más simple, pero no por ello
menos importante. En la naturaleza, la luz se mueve en línea recta con
velocidad constante de 300.000 km/s, y no hay manera de exagerar la importancia
que tiene para la vida. También es posible modelar el sonido, cuya velocidad es
343 m/s en el aire, a una temperatura de 20 ºC.
La ecuación de la posición ‘x’ en función del
tiempo ‘t’ para el movimiento rectilíneo uniforme también es muy simple:
x (t) = xo + vt
Donde ‘x o’ es la posición inicial
del móvil y ‘v’ es su velocidad. Esta es la ecuación de una recta que pasa por
x o y cuya pendiente es v, la cual puede
ser positiva o negativa.
Gráfica de la posición versus el tiempo x (t)
Gráficamente se muestran estos dos casos en la siguiente figura. A la izquierda, un móvil con velocidad positiva, el cual se aleja del origen (pendiente ascendente), y a la derecha, uno con velocidad negativa (pendiente descendente), que se acerca al origen. El ángulo α es el ángulo que forma la recta con el eje x positivo e indica la pendiente de la recta.
Cuando α se mide por encima del eje x
positivo, la velocidad es positiva, mientras que,
si se mide por debajo, es negativa.
 |
| Fuente: Wikimedia Commons. |
Gráfica de la velocidad versus el tiempo v(t)
Puesto que en el movimiento rectilíneo uniforme la velocidad es constante, su gráfica en función del tiempo será una recta horizontal (paralela al eje x):
Tiene sentido, porque lo que este gráfico está indicando es que la velocidad
conserva el valor que tiene, sin importar el tiempo transcurrido.
Si la velocidad es positiva, la línea recta se
encontrará por encima de y = 0, como en la figura mostrada arriba. Pero
si la velocidad es negativa, estará por debajo de y = 0.
Cálculo de la distancia recorrida a partir de la
gráfica v (t)
Si se dispone de la gráfica v(t) de un móvil
con movimiento rectilíneo uniforme, la distancia recorrida en un determinado
intervalo de tiempo equivale al área bajo la gráfica determinada por dicho
intervalo. En la imagen de arriba, se muestra que la distancia recorrida hasta
el tiempo ‘t o’ equivale al área del rectángulo mostrado, en la cual
la distancia se denota como ‘s’ (space). Nótese que en la fórmula
mostrada se ha considerado la posición inicial so como igual a 0.
Ejemplo resuelto 1
La siguiente gráfica muestra la posición versus el tiempo para los móviles 1 y 2 que se mueven a lo largo de la recta dada por el eje x.
A) ¿Qué tipo de movimiento tienen?
B) ¿Cuál de ellos tiene mayor velocidad?
C) ¿Qué representan los puntos de intersección con el eje vertical?
Respuesta A
Ambos móviles tienen movimiento rectilíneo
uniforme, ya que sus respectivas gráficas de posición versus tiempo son líneas
rectas.
Respuesta B
El móvil 2 es el que tiene mayor velocidad,
puesto que su pendiente es mayor.
Respuesta C
El punto de intersección con el eje vertical
coincide en ambos casos, esto significa que los móviles tienen el mismo punto
de partida. Además, ambos partieron en el instante t = 0,
Ejemplo resuelto 2
A continuación, se muestra la gráfica de dos
móviles con movimiento rectilíneo uniforme. Calcular:
A) La velocidad de cada uno.
B) ¿Qué distancia los separa al cabo de 2 segundos? ¿Y al cabo de 4 segundos?
C) ¿Cuánto tarda el móvil 1 en llegar a x =
7m? ¿Y cuánto tarda el móvil 2 en llegar a esa misma posición?
Respuesta A
Dado que la velocidad equivale a la pendiente de la
recta, viene dada por la fórmula:Por lo tanto, hay que seleccionar dos puntos
de cada recta, pero como ambas pasan por el punto (0,0), se puede tomar ese
como el punto (t1, x1), quedando el punto (t2,
x2) a elección.
Para el móvil 1
Se toma como (t2; x2) al
punto (4s; 3m) y al sustituir en la fórmula, queda:
Para el móvil 2
El procedimiento es análogo, en este caso, se
elige el punto (4s; 6m)
Respuesta B
Las respuestas se obtienen leyendo el gráfico
cuidadosamente. Es importante destacar que, en este gráfico, la posición se lee
del eje vertical, mientras que el tiempo se lee en el eje horizontal.
Al cabo de t = 2 s, el móvil 1 se encuentra en
x = 1.5 m, mientras que el móvil 2 está en x = 3 m, por lo tanto, están
separados una distancia Δx = 3 m – 1.5 m = 1.5 m.
Mientras que, al cabo de t = 4 s, el móvil 1
está en x = 3m, y el móvil 2 está en x = 6 m, por lo tanto, están separados una
distancia Δx = 6 m – 3 m = 3 m.
Respuesta C
Observando atentamente el gráfico, y ayudándose con las cuadrículas, se observa que el móvil 1 llega a x = 7 m aproximadamente al cabo de t = 9.25 s, mientras que el móvil 2, al ser más rápido, llegó allí al cabo de t = 4.5 s aproximadamente.
Ejemplo resuelto 3
La siguiente es la gráfica velocidad tiempo de
un móvil con movimiento rectilíneo uniforme, en unidades del Sistema Internacional. Determinar:
A) La velocidad del móvil
B) Distancia recorrida al cabo de t = 3s
C) Distancia recorrida entre t = 2 s y t = 6 s
Respuesta A
Del gráfico puede leerse directamente que la
velocidad del móvil es de 10 m/s.
Respuesta B
La distancia recorrida equivale numéricamente
al área del rectángulo de base 3 s, y altura 10 m/s. El área de un rectángulo
es simplemente el producto de base por su altura, así:
D = 10 m/s × 3s = 30 m
Respuesta C
La distancia recorrida en el intervalo
solicitado equivale numéricamente al área del rectángulo cuya base es 6s – 2s =
4s y cuya altura es 10m/s, por lo tanto:
D = 10 m/s × 4s = 40 m



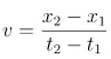







No hay comentarios:
Publicar un comentario