Los problemas de móviles en persecución son frecuentes en Física, y sirven para poner a prueba nuestra comprensión de los principios cinemáticos. Los móviles pueden ser autos o cualquier otro objeto, que normalmente se imagina como una partícula, con la finalidad de simplificar el análisis.
Las persecuciones y los encuentros aparecen en películas, series, juegos y en la vida real, como en esta persecución policial a lo largo de una avenida bastante recta de Chicago, Estados Unidos. Su modelado matemático a través de las ecuaciones de movimiento es bastante simple. Aquí lo mostramos en dos ejemplos resueltos paso a paso.
 |
| Créditos de la imagen: Eric Allix Rogers a través de Flickr. |
Ejercicio 1
Un auto pasa por un punto de la carretera a una velocidad de 20 m/s y 10 segundos más tarde, pasa por el mismo lugar una patrulla de la policía que lo va persiguiendo a una velocidad de 30 m/s. Si ambos móviles mantienen todo el tiempo la misma velocidad, encontrar a qué distancia del punto en cuestión se encuentran el conductor y la patrulla, y al cabo de cuánto tiempo se produce el encuentro.
Solución
Este problema trata de dos móviles en persecución, pero que no
pasan al mismo tiempo por el punto de referencia.
Lo primero que se debe hacer es determinar el tipo de movimiento de cada móvil, porque de esta manera se podrá elegir la ecuación más
conveniente. El enunciado afirma que los móviles mantienen sus velocidades
constantes, por lo tanto, el movimiento de cada uno es MRU, es decir,
movimiento rectilíneo uniforme.
Enseguida se escoge un punto de referencia, el cual
será ese punto de la vía al que hace referencia el enunciado.
A dicho punto se le asigna la coordenada x = 0 m, pero como
los móviles no pasan al mismo tiempo por ese punto, podemos decir que el
automovilista pasa por allí justo cuando se comienza a estudiar el movimiento, es
decir, en t = 0 segundos. Por su parte, la patrulla pasa con 10 segundos de
retraso.
Si el automovilista es el móvil 1, y t1 es su
tiempo, podemos decir que t1 = t, tomándolo a él como referencia.
Entonces t2 es el tiempo de la patrulla y t2 = t−10
segundos, ya que la patrulla siempre tiene retraso de 10 segundos (el signo
negativo antepuesto a 10 segundos da cuenta de ese retardo).
Tomando en consideración todo lo antes dicho, se parte de la
ecuación de movimiento para el MRU:
x(t) = x0 + v∙t
Y se adapta a cada móvil:
Móvil 1: el automovilista
x1(t) = x0 + v∙t
Con x0 = 0, ya que todo el movimiento comienza a
observarse en ese punto que menciona el enunciado, al cual se le ha dado el
valor de 0 m. Por lo tanto:
x1(t) = 20∙t
Móvil 2: la patrulla
x2(t) = 30∙(t −10)
Ahora se igualan ambas ecuaciones:
x1(t) = x2(t)
Lo que conduce a:
20∙t = 30∙(t−10)
20∙t = 30∙t −300
−10∙t = −300
t = 30 s
Se concluye que el auto y la patrulla se encuentran al cabo
de 30 s, luego de pasar por el punto de referencia. Ahora, para saber a cuántos
metros de dicho punto se produce el encuentro, basta sustituir este tiempo en
cualquiera de las ecuaciones del movimiento, por ejemplo, en x1:
x1(t) = 20∙t = 20 m/ s ∙ 30 s = 600 m
Es muy sencillo verificar estos resultados mediante la
gráfica de la posición versus el tiempo para ambos móviles:
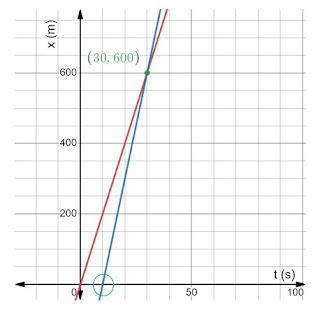
La gráfica correspondiente al móvil 1, el automovilista, se
representa en rojo, mientras que la de la patrulla se dibujó en azul. Obsérvese
que la recta del automovilista pasa por el origen, pero la de la patrulla parte
de t = 10 segundos, como se señala en el círculo verde.
El punto de intersección es (30 s, 600 m), lo cual coincide con los cálculos previos.
Ejercicio 2
Un camión que viaja a 30 millas/h
pasa de largo un semáforo en rojo en una avenida larga y recta. Mientras tanto,
un automovilista que esperaba tranquilamente, al verse rebasado por el camión,
asume que la luz ha cambiado y arranca con aceleración constante de 12 pies/seg 2. Dos segundos después, un oficial en motocicleta oculto en la
intersección, sale del reposo con una aceleración constante y desconocida.
Si el oficial desea atrapar a ambos infractores, ¿cuál debe ser el valor de su aceleración para llegar al automovilista justo cuando está rebasando al camión?
 |
| Fuente: Pxhere |
Solución
Aquí tenemos tres móviles, aunque por el momento basta con
preocuparse por los dos primeros: el camión C, cuyo movimiento es rectilíneo
uniforme, y el automovilista A, que tiene movimiento rectilíneo uniformemente
acelerado.
Todo comienza en el semáforo, cuya ubicación será x = 0, y
el tiempo t= 0 s es aquel en el cual el auto es rebasado por el camión. Las
unidades serán pies y segundos, por lo tanto, hay que convertir la velocidad
del camión:
vC
= 30 millas/h = 40 pies/s
La siguiente tabla es de utilidad para organizar la
información que ofrece el enunciado:
Móvil C: el camión
xC(t) = x0 + v∙t
xC(t) = 40∙t
Móvil A: el automovilista
xA(t) = x0 + v0∙t+ ½ aAt2
Con v0 = 0 ya que parte del reposo y aA
= 12 pies/seg 2, según dice el enunciado:
xA(t)
= ½ 12t2
= xA(t) = 6t2
En seguida, se plantea la igualdad en ambas:
xC(t) = xA(t)
40∙t = 6t2
Lo cual conduce a:
6t = 40 → t = 6.7 s
La posición del encuentro ocurre en:
xC(t) = 40∙t = 40∙6.7 pies = 266.7 pies
Si se prefiere, se puede calcular la posición del encuentro a
través de la ecuación del automovilista. Normalmente aparecen pequeñas
diferencias en el resultado, debido al redondeo en las operaciones.
Los resultados se verifican con ayuda de una calculadora gráfica:
El móvil azul se representa en color azul y su gráfica es
una parábola, mientras que el camión va en rojo y su gráfica es una recta. Nótese
que hay dos intersecciones: (0,0) que se produce cuando se encuentran delante
del semáforo, y la que ocurre posteriormente, en (6.7; 266,7). Tras eso, los móviles
no vuelven a encontrarse de nuevo, si mantienen el mismo
movimiento.
Ahora vamos a introducir al tercer móvil, el móvil P o patrulla,
cuyo movimiento es rectilíneo uniformemente acelerado, la cual parte del reposo
(v0) en la intersección y con 2 segundos de retardo. Entonces su
ecuación es:
Móvil P: la patrulla
xP(t) = ½ aP(t−2)2
Como la patrulla intercepta a los otros dos, se deben
encontrar en xP = 266.7 pies y t = 6.7 s, con estos valores:
266.7 = ½ aP(6.7−2)2 = ½ aP(4.7)2
= 11.045 aP
Por lo tanto:
aP = 24.1467 pies/s2
Veamos cómo quedan las tres gráficas superpuestas, porque a partir
de ella se encontrarán algunos detalles interesantes.
Si todos los cálculos son correctos, las tres gráficas deberían interceptarse
todas en el punto en cuestión.
Pero antes, hay que construir la ecuación para la patrulla con
ayuda de este resultado:
xP(t)
= ½ aP(t−2)2 = ½ ×24.1467× (t−2)2 = 12.0733(t−2)2
Ahora se ha agregado la curva correspondiente a la patrulla, en
color verde:
Se observa que la gráfica de este tercer móvil también es una parábola, lo cual era de esperar, ya que su movimiento es rectilíneo uniformemente acelerado, al igual que el del automovilista, pero con diferente aceleración y además, su vértice está desplazado t = 2 segundos a la derecha, puesto que partió con retardo.
Lo siguiente es que la curva verde intercepta a las otras dos simultáneamente en
el mismo punto calculado antes, por lo cual respiramos tranquilos, sabiendo que los resultados son correctos.
Pero además corta a las otras dos en distintos instantes, ambos previos al encuentro final, lo cual significa que la patrulla los rebasó por separado antes de encontrárselos a los dos.
Al camión lo
rebasó al cabo de t = 0.595 segundos, mientras que al automovilista lo hizo
luego de t = 1.173 segundos. Estos resultados se obtuvieron de la gráfica, pero se pueden confirma haciendo las intersecciones de la patrulla y el camión, y la patrulla con el automovilista, por separado. Es decir, hay que plantear y resolver estas ecuaciones:
xP(t) = xC(t)
Y




No hay comentarios:
Publicar un comentario