En esta breve revisión, se verá cómo Newton hizo uso de sus tres leyes del movimiento y de la tercera ley de Kepler, para encontrar la expresión que permite calcular la fuerza de atracción gravitatoria existente entre dos objetos cualesquiera con masa.
Esos dos objetos pueden ser, por ejemplo, la Tierra y el
Sol. En principio y por simplicidad, se puede suponer que la órbita de la Tierra
alrededor del Sol es circular, aunque en realidad es elíptica, solo que la
excentricidad de esta elipse es tan pequeña, que es casi como si fuera una
circunferencia.
Enseguida se aplica la segunda ley de
Newton, según la cual, la magnitud de la fuerza centrípeta Fc
es el producto de la masa m de la Tierra por su aceleración centrípeta ac:
Donde k es la constante de
proporcionalidad.
Sustituyendo estas dos ecuaciones en la expresión
para la magnitud de la fuerza centrípeta, se obtiene lo siguiente:
Y de acuerdo a esto, la fuerza que
mantiene a la Tierra en órbita alrededor del Sol, debe ser inversamente
proporcional al cuadrado de la distancia entre ambos objetos celestes.
Considerando la tercera ley de Newton, el
cuerpo que ejerce la fuerza sobre la Tierra, que en este caso es el Sol, recibe
una fuerza que es igual en magnitud a Fc, en la misma
dirección y en sentido contrario. La magnitud de dicha fuerza es proporcional a
M, la masa del Sol, por lo que se puede escribir una ecuación parecida a la
anterior, pero con una constante de proporcionalidad diferente, a la cual
llamaremos k’:
Si se multiplica Fc por
m, la masa de la Tierra, se altera la ecuación, pero entonces la fuerza queda
expresada en términos de las masas involucradas. Para evitar que se altere,
dado que las masas son constantes, se coloca una tercera constante k’’
diferente de las anteriores, pero relacionada con ellas:
No hay problema con esto, pues las
constantes se reúnen bajo un mismo nombre, G, obteniéndose:
¡Y por fin!, la magnitud de la fuerza de atracción
gravitacional entre m y M resulta la conocida ecuación:
Con el valor de G en el Sistema
Internacional de Unidades dado por:
G = 6.673 × 10−11 N∙m2/kg2
Esta es la ley de gravitación universal de Newton, según la cual dos objetos de masas m y M, separados una distancia r, se atraen con una fuerza proporcional al producto de las masas e inversamente proporcional al cuadrado de la distancia que las separa.
Dado que la fuerza es un vector, en principio, la fuerza está dirigida a lo largo de la línea que une los respectivos centros. En otras palabras, se supone que los objetos son partículas, aunque en realidad tengan tamaño mensurable.
No necesariamente estos objetos tienen que ser planetas y estrellas, u
objetos celestes en general. La fuerza de gravedad atrae a cualesquiera dos masas en
cualquier parte, solo
que, si las masas son muy pequeñas, la fuerza de atracción también lo será.
 |
| Esquema de la atracción gravitatoria entre dos masas. Fuente: Wikimedia Commons. |
Ejemplo 1
 |
¿Con qué aceleración cae la manzana? Fuente: Pexels. |
Respuesta
Se sabe que el objeto caerá hacia el
centro de la Tierra con la aceleración de gravedad g. En la ecuación
anterior, diremos que m es la masa del objeto, mientras que M es
la masa de la Tierra, además r será igual a:
r = h + R
Pero h es mucho, pero mucho menor
que R, puesto que el radio de la Tierra es de aproximadamente R = 6371
km = 6378000 m. Por lo tanto, no nos arriesgamos al afirmar que:
h + R ≈ R
Después de todo, si le sumamos a un número muy grande como R, otro número muy pequeño en comparación, como h, la diferencia no es mucha y el resultado seguirá siendo R con muy buena aproximación. El lector puede comprobar que esto es cierto con la ayuda de su calculadora.
Por eso utilizamos el símbolo ‘≈’, para indicar
que se trata de una aproximación, que en la práctica resulta muy conveniente, como se verá en breve.
Aplicando la segunda ley de Newton:
Entonces:
Ejemplo 2
.jpg) |
El planeta Gliese 581c se encuentra en la zona habitable de su estrella, la enana roja Gliese 581, situada a 20.5 años luz de la Tierra. Fuente: Wikimedia Commons. |
La ecuación deducida anteriormente dará la respuesta, despejando la masa del planeta, que en este caso llamaremos como MG, con el subíndice ‘G’ que indica ‘Gliese’:
Con la información del enunciado y los
valores de radio y gravedad terrestre, se tiene:
RG = 1.5 × 6378000
m
gG = 2.2 × 9.8m/s2
Gliese 581c es un planeta rocoso, semejante a la Tierra,
aunque de mayor tamaño. Su densidad aproximada es de 8.1 kg/m3, un
valor que se puede calcular fácilmente, ahora que se conoce la masa del
planeta.
¿Cómo sería vivir allí?
Por F. Zapata






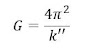







No hay comentarios:
Publicar un comentario