Ejercicio 1
Segunda ley de Newton
Un auto con una masa de 1.000,0 kg acelera de 0 a 90,0
km/h en 10,0 s. Calcular:
a) La magnitud de su aceleración
b) La magnitud de la fuerza neta sobre el auto?
 |
| Fuente: Pixnio. |
Solución a
La aceleración media del auto am se puede calcular mediante:
Pero antes es necesario unificar las
unidades, por ejemplo, pasando los 90 km/h a m/s:
90 km/h = 25 m/s
Por lo tanto:
Solución b
De acuerdo a la segunda ley de Newton, la magnitud de la fuerza FN viene dada por:
FN = m∙a
Sustituyendo valores:
FN = 1000 kg ∙ 2.5
m/s2 = 2500 N
Ejercicio 2
Segunda ley de Newton
Sobre una partícula de masa 2,0 kg actúa una fuerza única y constante, dada por F = 18 i N. Hallar:
a) El vector aceleración de la partícula
b) Si la partícula parte del reposo, ¿qué distancia recorre en los primeros 5,0 s?
Solución a
De acuerdo a la segunda ley de Newton:
Solución b
Dado que la aceleración de la partícula
es constante, su movimiento es rectilíneo uniformemente variado, por lo tanto,
al sustituir valores se tiene:
d = ½ at2 = ½
×
9 m/s2 × (5 s)2 = 112.5 m
Ejercicio 3
Componentes de una fuerza
La componente Fx de cierta fuerza F es igual a 120 lb y se sabe que la componente Fy es negativa. Si la magnitud de F es de 150 lb, hallar:
a) El valor de la componente Fy en lb y en N.
b) Determinar una expresión para F.
Solución a
La fuerza buscada es de la forma F = Fx i + Fy j, ya que solo tiene dos componentes, y su magnitud viene dada por:
Usando la equivalencia entre libra y newton se obtiene:
90 lb = 400.34 N
Solución b
El vector F queda expresado así:
F = 120 i – 90 j lb = 533.79 i – 400.34 j N
El signo negativo que se antepone a la componente Fy proviene de la información dada por el enunciado, según la cual dicha componente es negativa.
Ejercicio 4
Sumatoria de fuerzas por componentes
La suma vectorial del sistema de fuerzas coplanares y concurrentes de la figura es nula. Las magnitudes de FB, FC y FD son conocidas. Calcular la magnitud de FA y el valor del ángulo α.
FB = 800 lb; FC = 1000 lb; FD = 900 lb
 |
| Fuente: Bedford. Estática. |
Solución
Este problema se resuelve fácilmente hallando la fuerza resultante e igualando su magnitud a 0, con el método de las componentes, ya que se conocen los ángulos y las magnitudes para tres de las fuerzas que participan:
FAx = − FA ∙ cos α
FAy = − FA ∙ sen α
FBx = − FB ∙ cos 70º = − 800 ∙ cos 70º lb = − 273.62 lb
FBy = FB ∙ sen 70º = 800 ∙ sen 70º lb = 751.75 lb
FCx = FC ∙ cos 30º = 1000 ∙ cos 30º lb = 866.03 lb
FCy = FC ∙ sen 30º = 1000 ∙ sen 30º lb = 500.00 lb
FDx = FD ∙ cos 20º = 900 ∙ cos 20º = 845.72 lb
FDy = −FD ∙ sen 20º = − 900 ∙ sen 20º = − 307.82 lb
De inmediato se encuentra la sumatoria de todas las fuerzas a lo largo el eje x y se iguala a 0:
∑ FRx = −FA ∙ cos α − 273.62 + 866.03 + 845.72 = 0
Y se obtiene la siguiente ecuación:
−FA ∙ cos α = 273.62 − 866.03 − 845.72 lb = −1438.13 lb
FA ∙ cos α = 1438.13 lb
Se lleva a cabo un procedimiento análogo para las fuerzas sobre el eje y:
∑ FRy = −FA ∙ sen α + 751.75 + 500.00 − 307.82 lb= 0
− FA ∙ sen α = − 751.75 − 500.00 + 307.82 lb = − 943.18 lb
FA ∙ sen α = 943.18 lb
Y ahora se dividen los resultados obtenidos:
Por lo tanto, α = 33.3º
Una vez conocido el ángulo, ya se puede despejar la magnitud de FA:
FA ∙ sen α = 943.18 lb
FA ∙ sen 33.3º = 943.18 lb → FA = 1718 lb
Ejercicio 5
Diagrama de cuerpo libre
 |
| Bloque sobre plano inclinado. Fuente: Wikipedia. |
Solución
Dado que el bloque está en reposo, solo puede ser mantenido de esta forma por el rozamiento estático f, que se opone a que el bloque resbale cuesta abajo, equilibrando a la componente del peso W paralela al plano inclinado. La otra fuerza actuando sobre el bloque es la normal N.
Ejercicio 6
Diagrama de cuerpo libre
En la siguiente imagen se muestra un bloque que desliza cuesta abajo sobre un plano inclinado rugoso. Dibujar el diagrama de cuerpo libre que corresponde a esta situación.
Solución
En este caso, sobre el bloque siguen actuando el peso W y la normal N. Como el plano inclinado es rugoso, también está presente el roce, pero en ese caso actúa el rozamiento cinético f, en vista de que el bloque se está moviendo. Esta fuerza se opone a que el bloque resbale cuesta abajo, más no lo impide.
Si el roce cinético equilibra a la componente horizontal del peso, el bloque se mueve cuesta abajo con velocidad constante, de lo contrario el bloque tiene aceleración.
Ejercicio 7
Diagrama de cuerpo libre
Ejercicio 8
Segunda ley de Newton y diagrama de cuerpo libre
¿Qué fuerza deberá
aplicarse a un cajón de 100,0 kg en un plano sin fricción inclinado
a 30° para provocar una aceleración de 2,0 m/s2 hacia
arriba?
 |
| Fuente: Open Stax Physics Course. |
Solución
El diagrama de cuerpo libre es:
 |
| Fuente: Open Stax Physics Course. Modificado por F. Zapata. |
Se descompone el peso, por estar inclinado respecto al
sistema de referencia seleccionado en la figura. Nótese que W forma un
ángulo de 30º con respecto al eje vertical negativo (¿por qué? En caso
de duda, revisar cuidadosamente el post del plano
inclinado paso a paso)
Por lo tanto:
∑ Fy = N – Wy = 0
Se toma como sentido positivo el vertical hacia arriba.
La sumatoria se iguala a 0, puesto que el cajón no se mueve a lo largo
del eje y.
Para el eje horizontal, en el cual sí hay aceleración, la sumatoria de fuerzas es:
∑ Fy = F – Wx = ma
Se toma como sentido positivo el del movimiento. Entonces:
F = ma + Wx
Las componentes del peso son:
Wy
= 100,0 kg × 9.8 m/s2 × cos 30º = 848.7 N
Wx = 100,0 kg × 9.8 m/s2 × sen 30º = 490.0 N
Sustituyendo valores:
F = 100,0 kg ×2,0m/s2 + 490.0 N = 200.0 N + 490 N = 690 N
Ejercicio 9
Segunda ley de Newton y diagrama de cuerpo libre
El bloque de la figura pesa 200 N y está sujeto al techo mediante cuerdas que forman los ángulos mostrados en la figura. Calcular las magnitudes de las tensiones T1, T2 y T3 para que el bloque permanezca en equilibrio estático.
Solución
En primer lugar, se dibujan los diagramas de cuerpo libre para el bloque (izquierda) y el nudo (derecha). El peso de bloque se representa mediante W:
Del diagrama de cuerpo libre del bloque se obtiene una ecuación, aplicando la condición de equilibrio:
∑ Fy = 0
T3 – W = 0
La cual permite conocer la magnitud de T3:
T3 = W = 200 N
Y del diagrama de cuerpo libre del nudo resultan dos ecuaciones escalares para las componentes a lo largo del eje x y a lo largo del eje y, respectivamente.
∑ Fx = T2 ∙ cos 30º − T1 ∙ cos 40º = 0
∑ Fy = T1 ∙ sen 40º + T2 ∙ sen 30º − T3 = 0
Resulta un sistema de dos ecuaciones con dos incógnitas:
0.64 T1 + 0.50 T2 = 200
− 0.77T1 + 0.87 T2 = 0
Cuya solución es:
T1 = 184.8 N
T2 = 163.5 N
Ejercicio 10
Problema con dos masas y cuerdas
Se cuelgan dos masas m1 = 5 kg y m2 = 8 kg de las cuerdas livianas, homogéneas e inextensibles mostradas en la figura, de manera que el sistema está en equilibrio estático. ¿Cuáles son las tensiones en cada cuerda? La cuerda DC es capaz de soportar una tensión máxima de 140 N, ¿a partir de qué valor de m2 romperá la cuerda?
Solución
Se observa que todas las fuerzas están dirigidas verticalmente, algunas hacia arriba y otras hacia abajo. Se le asigna el signo + a las fuerzas que apuntan hacia arriba, y signo — a las que apuntan hacia abajo.
Dichas fuerzas son las siguientes:
Sobre m1
- TCD (rojo)
- W1 (naranja)
- TBA (verde)
Sobre m2
- TAB (verde)
- W2 (morado)
Nótese que las tensiones TAB y TBA tienen la misma magnitud:
TBA = TAB
Enseguida se aplica la segunda ley de Newton a cada masa:
Puesto que el peso es el producto de la masa por la aceleración de la gravedad, se tiene:
- W1 = 5 kg × 9.8 m/s2 = 49.0 N
- W2 = 8 kg × 9.8 m/s2 = 78.4 N
De la segunda ecuación se deduce fácilmente que:
TAB = W2 = 78.4 N
Mientras que de la primera:
TCD = TAB + W1
TCD = 78.4 N + 49.0 N = 127.4
Puesto que este valor es menor a 140 N, la cuerda CD no se rompe, para que eso suceda, hagamos TCD exactamente igual a 140 N, dejando fijo el valor de m1 y despejando TAB en ese caso:
TAB = TCD – W1 = 140 N — 49.0 N = 91 N
Y se sustituye este valor en la segunda ecuación, para despejar W2:
W2 = TAB = 91 N
Como W2 = m2g= 91 N, entonces:
m2 = 91 N/9.8 m/s2 = 9.3 kg
Entonces, al colgar una masa de 9.3 kg o mayor, la cuerda CD se romperá.
Ejercicio 11
Objeto en equilibrio estático
¿Cuáles son las magnitudes de las tensiones en las cuerdas livianas para que el motor de la figura se mantenga suspendido en equilibrio? El aro A por el que pasan las cuerdas también es liviano.
Solución
El motor puede considerarse como una partícula suspendida en equilibrio estático a través de la cuerda AC. En tal caso, esta soporta un peso de 2452 kN (se lee ‘kilo newton’), y la tensión a través de ella será igual a este valor. Las tensiones en las cuerdas AD y AB serán diferentes, para hallarlas, se requiere el diagrama de cuerpo libre en el aro liviano A:
La tensión TD se encuentra a lo largo del eje horizontal en sentido negativo y se le asigna signo —, entonces se puede escribir:
TD = TDx
No está demás insistir en el hecho de que un vector se denota con letra negrita, mientras que su magnitud, que es un escalar, se denota con letra común.
Por su parte, la tensión TB está en el plano xy y tiene dos componentes, que por trigonometría elemental, son:
- TBx = TB × cos 30o = 0.87 TB
- TBy = TB × sen 30o = 0.50 TB
La ecuación:
Es vectorial, lo cual significa que, en el caso de dos dimensiones, se desglosa en dos ecuaciones:
- TBx — TDx = 0
- TBy — 2452 = 0
De esta última es inmediato deducir que:
TBy = 2452 kN
Y puesto que TBy = 0.50 TB, se concluye que:
TB = 2452 kN / 0.5 = 4904 kN
Mientras que de TBx — TDx = 0, se desprende que:
TDx = TBx
Por lo tanto:
TDx = 0.87 TB = 0.87× 4904 kN = 4266.5 kN
Solución alternativa mediante el teorema de Lamy
Las tres fuerzas del diagrama de cuerpo libre del anillo son coplanares y concurrentes, por lo tanto, el teorema de Lamy se puede aplicar para determinar sus magnitudes. El teorema dice así:
 |
Tres fuerzas coplanares y concurrentes, a las cuales se puede aplicar el teorema de Lamy. Fuente: Wikimedia Commons. |
Comparando cuidadosamente esta figura con la del diagrama de cuerpo aislado del aro a través del cual pasan las cuerdas, se llega a la siguiente conclusión:
Importante: en ambas soluciones se utilizaron los valores sen 30º = 0.5; cos 30º= 0.87, téngase presente que las calculadoras ofrecen más decimales para el coseno de 30º y que, por lo tanto, los resultados pueden variar ligeramente. La persona que lleva a cabo los cálculos es quien decide cuántos decimales necesita tomar.
Ejercicio 12
Problema con dos masas y una polea ideal
Dos bloques están conectados por una cuerda liviana como se muestra a continuación. La masa del bloque sobre la mesa es de 4,0 kg y la masa colgante es de 1,0 kg. No hay fricción entre la mesa y la polea, ni entre el bloque ni la mesa. Calcular:
a) La aceleración del sistema.
b) Halle la tensión en la cuerda.
c) Halle la rapidez con la que la masa colgante golpea el suelo si parte del reposo y se sitúa inicialmente a 1,0 m del suelo.
 |
| Fuente: Open Stax Physics Course. |
Solución a
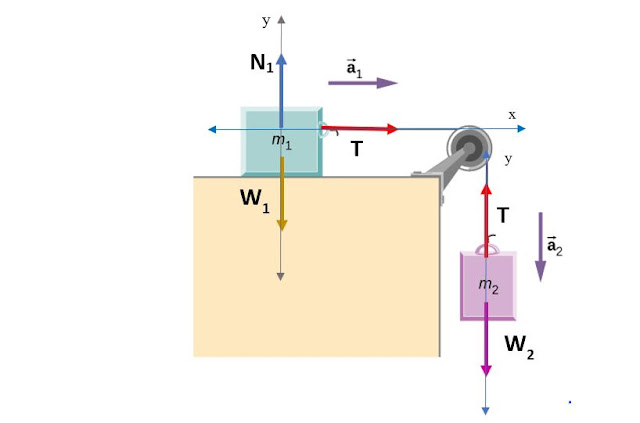 |
| Fuente: Open Stax Physics Course. Modificado por F. Zapata. |
Es importante observar que la tensión en la cuerda es la
misma para cada cuerpo, dado que la cuerda es liviana e inextensible, y la
polea es ideal, por lo tanto, carece de roce y es muy liviana. En lo que sigue,
se escoge la dirección del movimiento de cada masa como positiva, la cual
también aparece señalada en el diagrama.
Ahora se aplica la segunda ley de Newton para cada masa,
tomando en cuenta que los bloques se mueven con la misma aceleración ‘a’:
Para m1
∑ Fy = N – W1 = 0
∑ Fx = T = m1 a
Para m2
∑ Fy = T – W2 = – m2 a
Enseguida, se plantea un sistema de dos ecuaciones con dos
incógnitas, que serán ‘T’ y ‘a’:
El sistema se resuelve fácilmente
sustituyendo la primera ecuación en la segunda:
m1a – W2 = – m2a
m1a + m2a = W2
Y de aquí resulta el siguiente valor para
la aceleración:
Solución b
El valor de la tensión se encuentra sustituyendo el valor de
la aceleración calculado antes:
Solución c
El movimiento de los bloques es rectilíneo uniformemente
acelerado, con la aceleración calculada anteriormente. Puesto que el bloque
parte del reposo y recorre 1 m antes de llegar al suelo, la velocidad con que golpea
puede calcularse a partir de:
Sustituyendo valores:
Ejercicio 13
Problema de plano inclinado con roce
Un esquiador, cuya masa es de 67 kg está esquiando sobre una cuesta con rozamiento, cuya inclinación respecto a la horizontal es de 37º.
Calcular:
a) La magnitud de la fuerza de fricción si se sabe que el coeficiente de fricción cinética entre la superficie de los esquíes y la nieve es 0.07.
b) La magnitud de la aceleración del esquiador al descender por la cuesta.
 |
| Un esquiador desciende por una cuesta, tomando en cuenta el efecto de la fricción. A la derecha está el diagrama de cuerpo libre. Fuente: Open Stax Physics Course. Modificado por F. Zapata. |
Solución a
En la figura de arriba está el diagrama de cuerpo libre. Las consideraciones para resolverlo son las mismas que las de la máquina simple llamada plano inclinado, aquí está el link del paso a paso para resolver el problema del plano inclinado. Será preciso aplicar las leyes de Newton y el primer paso, como siempre es encontrar las componentes del peso, que es la única fuerza inclinada, según el sistema de coordenadas seleccionado. La magnitud del peso del esquiador es: W = mg = 67 kg∙ 9.8 m/s2 = 656.6 N De acuerdo al diagrama de cuerpo libre, las componentes del peso son: Wx = mg∙ sen 37º = 656.6 N∙sen 37º = 397.0 N Wy = mg∙ cos 37º = 656.6 N∙cos 37º = 524.4 N Aplicando la segunda ley de Newton se tiene:
De la primera ecuación se despeja la magnitud de la normal: N = Wy = 524.4 N Y al aplicar la ecuación 2), dada más arriba para el cálculo de la fricción cinética, se obtiene: fk = μk ∙N = 0.07 ∙524.4 N = 36.7 N Solución bDe la ecuación 2 se despeja ax : |
El resultado es negativo, no hay problema con ello, pues en el diagrama de cuerpo libre se ha tomado como sentido positivo de las x al de la fricción (cuesta arriba). Ya que el esquiador desliza cuesta abajo, su aceleración tiene signo negativo.
Ejercicio 14
Ley de gravitación universal
Solución
Se sabe que el objeto caerá hacia el centro de la Tierra con la aceleración de gravedad g. En la ecuación anterior, diremos que m es la masa del objeto, mientras que M es la masa de la Tierra, además r será igual a:
r = h + R
Pero h es mucho, pero mucho menor que R, puesto que el radio de la Tierra es de aproximadamente R = 6371 km = 6378000 m. Por lo tanto, no nos arriesgamos al afirmar que:
h + R ≈ R
Después de todo, si le sumamos a un número muy grande como R, otro número muy pequeño en comparación, como h, la diferencia no es mucha y el resultado seguirá siendo R con muy buena aproximación. El lector puede comprobar que esto es cierto con la ayuda de su calculadora.
Por eso utilizamos el símbolo ‘≈’, para indicar que se trata de una aproximación, que en la práctica resulta muy conveniente, como se verá en breve.
Aplicando la segunda ley de Newton:
Entonces:
Ejercicio 15
Ley de gravitación universal
Solución
Despejando la masa del planeta de la ecuación del ejercicio anterior y denotándola como MG, con el subíndice ‘G’ por ‘Gliese’, queda:
Con la información del enunciado y los valores de radio y gravedad terrestre, se tiene:
RG = 1.5 × 6378000 m
gG = 2.2 × 9.8m/s2
Por F. Zapata
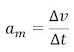



























No hay comentarios:
Publicar un comentario