Las potencias son una forma abreviada de escribir la multiplicación por sí mismo de un número base, tanto como lo indique otra cifra, llamada exponente.
Hasta donde sabemos, la primera referencia del concepto de potencia la dio Euclides, el notable matemático y geómetra de la antigua Grecia, quien llamó “potencia” al número de veces que un número cualquiera se multiplicaba consigo mismo.
Sea a la base, un número real y n el exponente, un número racional. En tal caso:
Esta expresión se lee como ‘a elevado a la n’.
Obsérvese que el exponente se escribe más pequeño y se ubica
arriba y a la derecha de la base, como un superíndice. No es la única
forma de denotar una potencia, pero sí la más utilizada en la literatura
algebraica. En cambio, en los lenguajes
de programación, la potencia se denota con el símbolo circunflejo “^” o el
doble asterisco, así:
A modo de ejemplo práctico, aquí se multiplica
el 3 consigo mismo 5 veces. En este caso, 3 es la base y 5 es el exponente:
35=
3∙3∙3∙3∙3=243
Leyes de los exponentes
1.- Regla del exponente cero
Cualquier base diferente de cero, elevada al
exponente cero, es igual a la unidad.
Ejemplos
20 =
1
(−5)0 =
1
1000
= 1
x0
= 1
2.- Regla del exponente uno
Toda base elevada al exponente uno es igual a
la base.
Ejemplos
(−4)1 = −4
251
= 25
(½)1
= ½
m1
= m
3.- Regla del producto
El producto de dos potencias de la misma base equivale a calcular la potencia de la misma base elevada a la suma de los exponentes:
Ejemplo
x3∙ x7 = x3+7 = x10
4.- Regla del cociente
El cociente de potencias con la misma base y exponentes diferentes equivale a otra potencia con la misma base elevada a la resta de los exponentes:
Ejemplo
5.- Regla de una potencia elevada a otra potencia
Una potencia elevada a un exponente es equivalente a otra potencia con la
misma base, cuyo exponente es la multiplicación de los exponentes originales:
Ejemplo
(x3)2
= x3∙2 = x6
6.- Regla del exponente negativo
Cuando el exponente es un entero negativo, la
potencia equivale a su inverso elevado al exponente con el signo positivo:
Ejemplo
7.- Regla de la potencia de un producto
Esta regla hace referencia a la potencia del
producto de dos bases. Sean a y b dos números reales, entonces:
Esto significa que, para elevar un producto a
una potencia, se elevan todos los factores dentro del paréntesis a la potencia indica
afuera.
Ejemplos
(x∙y)4 = x4∙y4
(5z)3 = 53∙z3
= 125 z3
(−2a−1b2)2=
(−2)2∙(a−1)2∙(b2)2 = 4∙ a−2∙ b4
Nótese que en el último ejemplo se puede combinar el resultado con la regla del exponente negativo, para obtener:

7.- Regla de la potencia de un cociente
Esta regla hace referencia al cociente entre
dos bases. Sean a y b dos números reales, con b ≠ 0,
entonces:
Ejemplo

En este ejemplo se ha combinado la regla de la potencia de un cociente con la regla de la potencia de una potencia y la del producto de potencias.
Ahora, obsérvese un nuevo ejemplo de esta regla, pero con exponente negativo:




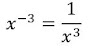


No hay comentarios:
Publicar un comentario