Los radicales o raíces son expresiones matemáticas muy utilizadas en álgebra, geometría, cálculo y otras disciplinas. En un radical, se distinguen el índice o grado n, el muy conocido signo radical, que denota la operación a realizar, y la cantidad sub-radical o radicando, que es la expresión o el número que se encuentra bajo el signo.
El siguiente es un ejemplo de radical, concretamente, de raíz cuadrada:
Más ejemplos de radicales con otros índices
son:
Nótese lo siguiente:
- Si el radicando es positivo y la raíz es par, hay dos soluciones reales y opuestas.
- Para radicandos negativos e índice par, no hay solución.
- Si el radicando es positivo o negativo, y la raíz es de índice impar, hay una solución con el mismo signo que lleva la cantidad subradical.
No siempre los radicales tienen como resultado un número entero o racional, y en tales casos, suele dejarse indicado, por ejemplo:
Es importante destacar que números como √2 no tienen una representación exacta en los números racionales, pero en forma decimal pueden escribirse de manera aproximada (no exactamente igual, ya que esto requeriría infinitos decimales):
Radicales como potencias
La radicación es una potenciación con exponente
fraccionario. En este caso, la raíz de cierto orden de un número, es
equivalente a elevar dicho número a la potencia inversa:De igual manera, cualquier expresión elevada a
un exponente fraccionario es igual a una raíz cuyo índice es el denominador y
cuya cantidad subradical está elevada a la potencia igual al numerador.
Ejemplos
Las leyes de los exponentes se cumplen también con la radicación cuando se piensa en este como exponente fraccionario.
1) Raíz de un producto
La raíz n-ésima de un producto es igual al producto de las raíces de los factores:
Donde a y b son números reales no negativos.
Ejemplo
2) Raíz de
un cociente
3) Raíz de
una raíz
Para calcular la raíz de una raíz se
multiplican los índices de las raíces y se conserva el radicando.
Simplificación de radicales
La simplificación de radicales se lleva a cabo dividiendo índice de la raíz y exponente de la cantidad subradical por el MCD (máximo común divisor) de ambos.
Ejemplo
Simplificar, si es posible, el siguiente radical:
Solución
MCD (21,9) = 3
Por lo tanto:
Extraer factores de un radical
Para extraer factores de un radical conviene descomponer la cantidad subradical convenientemente, buscando siempre que queden exponentes múltiplos del índice, ya que estos se pueden simplificar. Dentro del radical pueden quedar los exponentes que sean menores que el índice.
Ejemplo
Extraer todos los factores que sea posible del siguiente radical:
Solución
Introducción de factores en una raíz
Para introducir un factor dentro de una raíz, se eleva al índice y se multiplica por la cantidad subradical.
Ejemplo
Introducir al radical los factores que se encuentren fuera en la siguiente expresión:
Solución
Ejemplo
Efectuar la siguiente operación:
Solución
Luego se procede a multiplicar los índices de
las raíces y efectuar las potencias indicadas en la cantidad subradical:
Convertir radicales a índice común
Mediante este procedimiento se convierten radicales de distinto índice a radicales equivalentes con igual índice.
Calcular el índice común, el cual es el mcm
(mínimo común múltiplo) de los índices.
Elevar las cantidades subradicales al índice que resulta de dividir el índice común entre el índice respectivo.
Ejemplo
Convertir a un índice común los radicales:
Solución
Ejemplo
Ordenar de mayor a menor los radicales:
Solución
Para comparar radicales de distinto índice, se
pasan todos al mismo índice y se comparan las cantidades subradicales. Aquel
radical que tiene la mayor cantidad subradical es el mayor:
mcm (3,5,15) = 15
El orden es:
Producto y cociente de radicales con distinto índice
Ejemplo
Efectuar la siguiente operación:
mcm (4,6)=12
Ejemplo
Efectuar la siguiente operación:
Solución
Radicales semejantes
Son aquellos radicales que tienen el mismo índice y la misma cantidad subradical. El coeficiente real que los multiplica puede ser diferente.
Por ejemplo, los siguientes radicales son semejantes:
En cambio, los siguientes radicales no son
semejantes:
Reducción de radicales semejantes
Los radicales semejantes se pueden reducir
sumándolos algebraicamente, pero cuando no son semejantes, la suma algebraica
debe quedar indicada.
Ejemplo
Efectuar:
Solución
Puesto que se trata de radicales semejantes, se suman algebraicamente los coeficientes:
Ejemplo
Efectuar:
Solución
En vista de que los radicales no son semejantes y ya se han simplificado al máximo, la suma se debe dejar indicada tal como está.
Ejemplo
Efectuar:
Solución
Las cantidades subradicales son distintas y,
en principio, parece que no son radicales semejantes, sin embargo, después de
descomponer cada cantidad subradical como producto de sus factores primos, se
obtiene:
28 = 22∙7
63 = 32∙7
Al aparecer radicales semejantes, es posible reducirlos y simplificar la expresión:
Por F. Zapata.



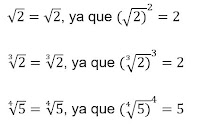














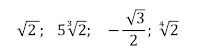
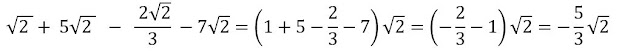
No hay comentarios:
Publicar un comentario