Las expresiones algebraicas consisten en combinaciones de letras y números, relacionadas mediante las operaciones ya conocidas en aritmética: adición, sustracción, multiplicación, división, potenciación y radicación.
Se componen de términos, conformados por grupos de letras y números. Los términos se suman o se restan. Las letras, a su vez, pueden adquirir valores numéricos que normalmente pertenecen el conjunto de los números reales, pudiendo estar elevadas a algún exponente entero o fraccionario. Y, asimismo, pueden estar multiplicadas por números reales.
 |
| El Álgebra es la base del Cálculo, la disciplina matemática imprescindible para modelar numerosos fenómenos naturales y situaciones en ciencia, ingeniería, economía y más. Fuente: Wannapik. |
Tipos de expresiones algebraicas
Existen diversos tipos de expresiones
algebraicas, de los cuales se describen seguidamente los más utilizados:
1)
Expresiones algebraicas enteras o
polinómicas
2) Expresiones
algebraicas racionales
Se forman mediante el cociente de dos expresiones algebraicas enteras, cuidando de que el denominador sea diferente de 0, (recuérdese que la división entre 0 no está definida).
Como ejemplo, se tienen las siguientes:
3)
Expresiones algebraicas radicales
Son expresiones algebraicas cuya parte literal es el argumento de una raíz, como en los casos a continuación:
4)
Expresiones algebraicas combinadas
Como su nombre lo indica, son expresiones algebraicas en las que se combinan dos o más tipos:
Términos semejantes
Son términos con la misma parte literal,
elevada a la misma potencia, y que solo difieren, si acaso, en el coeficiente.
Es importante reconocerlos rápidamente, pues tienen la ventaja de poderse reducir, como se verá enseguida.
Obsérvense los siguientes términos:
Son semejantes, ya la parte literal es la misma (la variable "x"), así como el exponente 2, aunque en cada caso, difiere en el coeficiente.
En cambio, los siguientes términos no son semejantes, pues la parte literal no está elevada a la misma potencia en ninguno de los casos.
Reducción de términos semejantes
Tal como se explicó anteriormente, los términos semejantes se pueden reducir. Es decir, se pueden sumar algebraicamente para obtener expresiones algebraicas más reducidas, con las cuales se puede trabajar más cómodamente. Para ello basta con sumar algebraicamente los coeficientes.
Ejemplo
Simplificar la siguiente expresión algebraica:
Solución
Dos de los términos tienen a la variable elevada a la misma potencia, lo que significa que son términos semejantes y, por lo tanto, se pueden reducir:
Lenguaje algebraico
Ciertas proposiciones pueden escribirse
mediante el lenguaje algebraico y así modelar matemáticamente numerosas
situaciones y problemas que se presentan en ciencias naturales, ingeniería,
economía y otras disciplinas. Para ello se utilizan las letras que designan a
las variables, que son normalmente las letras “x”, “y” y “z”, pero todas las
demás letras se pueden usar indistintamente.
Por ejemplo, la suma de dos números
cualesquiera se representa mediante:
En nuestros posts dedicados al lenguaje algebraico mostramos numerosos
ejemplos de cómo escribir proposiciones verbales, transformándolas en
ecuaciones sencillas. Acá están los enlaces:
https://www.todociencia.org/2022/09/como-usar-el-lenguaje-algebraico-con.html
https://www.todociencia.org/2020/04/problemas-de-lenguaje-algebraico.html
Valor numérico de una expresión algebraica
Consiste en sustituir ciertos valores en la
expresión algebraica y realizar las operaciones correspondientes, lo cual
conduce a un resultado numérico.
Ejemplo
a) Hallar el valor numérico de la expresión algebraica racional:
Solución
a
Sustituyendo x = 3, se obtiene:
Solución b
No es posible evaluar la expresión cuando x = 2, ya este valor anularía el denominador y, como se ha dicho antes, la división por 0 no está definida.
Ejemplo
a) Hallar el valor numérico de la expresión algebraica racional:
Solución a
Sustituyendo x = —1, resulta:
No hay problema que el numerador se haga 0, ya
que 0 dividido entre cualquier valor (no nulo) es igual a 0.
Solución b
Los valores
x = 2 y x = —3 anulan el denominador de la expresión original, por lo tanto, esta no se encuentra definida para ninguno de ellos. El lector puede comprobarlo intentando sustituir y evaluando con una calculadora. Para
Por F. Zapata.




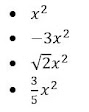

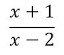



No hay comentarios:
Publicar un comentario