Se dice que los objetos de tamaño mensurable con carga eléctrica son distribuciones de carga continua. Tales distribuciones deben tener, al menos, una dimensión medible o mensurable.
 |
| Un alambre delgado cargado eléctricamente es una distribución de carga continua. Fuente: Flickr. |
La distribución de
carga continua más simple es el alambre o la varilla delgada cargada
eléctricamente. La carga puede distribuirse de manera equitativa a lo largo de
toda la longitud, o bien puede seguir alguna distribución particular, como por
ejemplo, concentrarse más en un extremo del alambre y menos en el otro, o
concentrarse en el centro.
En cada caso, el campo
eléctrico producido por dicha distribución será diferente, dependiendo de la
ubicación de la carga y el punto donde se quiera calcular el campo. Por
ejemplo, si la varilla o alambre tiene carga uniformemente distribuida, y el
punto de interés se localiza en el eje del alambre, a cierta distancia de un
extremo, no será igual el campo que produce allí el extremo más cercano del
alambre, que el que produce el extremo más lejano, como es lógico.
El extremo más lejano
produce un campo menos intenso, en razón de su lejanía, mientras que el extremo
más cercano produce un campo más intenso.
La pregunta que surge
es: ¿cómo tener en cuenta estas diferencias a la hora de calcular el campo
eléctrico? Después de todo, la ley de Coulomb se define, en principio, para
cargas puntuales, por lo tanto, ¿cómo se la puede aplicar para calcular el
campo eléctrico de un objeto continuo en un punto dado?
Estrategia para calcular el campo
eléctrico de una distribución continua
Es tan simple que se puede resumir en tres pasos:
- Se ‘divide’ (matemáticamente, claro está) el objeto en multitud de cargas minúsculas, que pueden considerarse ‘puntuales’.
- Se aplica a cada una de estas cargas la bien conocida ley de Coulomb para el campo eléctrico.
- Finalmente, se suman (vectorialmente) todos los campos eléctricos así obtenidos (¡hay que resolver una integral!) y ya se tiene por fin el campo eléctrico resultante en el punto en cuestión.
Ahora, hagamos un
gráfico que ilustre lo antes dicho. Se tiene un objeto con carga eléctrica Q,
distribuida sobre él, la cual, por comodidad, se supondrá positiva. El objeto
tiene una forma arbitraria.
Se toma una pequeña
porción del objeto, que contiene una pequeñísima porción de carga, la cual se
llamará dq. Este será nuestro diferencial de carga, representado
por el cubito en la parte superior del objeto en la figura de abajo.
Recuérdese que el campo eléctrico es un
vector, de allí que es necesario especificar siempre su dirección, por eso se
requiere escribir siempre el vector unitario respectivo. En el caso de
una distribución de carga positiva, el campo es saliente, mientras que si es
negativa, el campo es entrante a la misma.
 |
| Esquema de la aplicación de la ley de Coulomb para el campo eléctrico en una distribución de carga continua. |
El campo eléctrico
resultante en P, producido por todas las pequeñas contribuciones ubicadas en
los distintos lugares del objeto, hasta cubrirlo por completo, es la integral
efectuada sobre todo el volumen V del objeto.
Si el objeto no tiene
un volumen apreciable, pero sí una superficie S mensurable, la integral se hará
sobre dicha superficie:
Por último, si la
dimensión mensurable del objeto es su longitud L, como en el caso del alambre
mencionado al comienzo, la integral se llevará a cabo sobre dicha longitud.
Este es el procedimiento
general para trabajar con distribuciones de carga continua, ya que cada
caso tendrá su propia geometría, es decir, unos determinados dq y un r,
los cuales deberán expresarse convenientemente para poder calcular la
respectiva integral y obtener el campo.
Densidades de carga eléctrica
El concepto de densidad de carga, análogo al ya familiar de densidad de masa, ayudará a establecer el dq apropiado para calcular la integral del campo eléctrico.
En esta imagen se resumen las tres posibilidades geométricas discutidas en el apartado anterior: distribución lineal de carga, con una densidad de carga lineal, distribución superficial de carga, con una densidad de carga superficial y, por último, la distribución de carga volumétrica, son su densidad de carga volumétrica. |
| Fuente: hyperphysics. |
Se han elegido letras
griegas para simbolizar a cada densidad de carga, como se explica seguidamente:
Densidad de carga lineal
Se representa como λ, cuyas unidades son culombios por metro (C/m)
→ Cálculo de la carga
total
- Si la densidad es uniforme, el cálculo es muy simple:
Q=λ∙L
- Si la densidad es no uniforme, sino que depende de alguna coordenada espacial, digamos ‘x’, entonces hay que integrar sobre dicha dimensión, tomando una longitud infinitesimal sobre el alambre, dada por dx:
Donde L representa la longitud
total del alambre.
Densidad de carga superficial
Se representa mediante σ, cuyas unidades son culombios por metro cuadrado (C/m2)
En este caso:
- ‘dS’ es una superficie infinitesimal
- σ puede ser uniforme, o bien ser una función de las coordenadas espaciales.
→ Cálculo de la carga
total
- Si la densidad es uniforme:
Q=σ∙S
- Si la densidad es no uniforme, sino que depende de las coordenadas espaciales, digamos ‘x’ e ‘y’, entonces hay que integrar sobre la superficie S:
Donde dS representa una superficie muy pequeña del objeto
(infinitesimal).
Densidad de carga volumétrica
En este caso:
- ‘dV’ es un volumen infinitesimal
- ρ puede ser uniforme, o bien ser una función de las coordenadas espaciales.
→ Cálculo de la carga
total
- Si la densidad es uniforme:
Q=ρ∙V
- Si la densidad es no uniforme, sino que depende de las coordenadas espaciales, sino que depende de las coordenadas espaciales ‘x’, ‘y’ y ‘z’, por ejemplo, entonces hay que integrar sobre el volumen V:
Ejemplo 1
Distribución superficial de carga uniforme
Se tiene un disco de 5
cm de radio, con carga eléctrica positiva distribuida de manera uniforme en su
superficie a razón de 1.2 × 10-7 C/m2. ¿Cuál es la
carga total Q almacenada en el disco?
Solución
Dado que la carga está
distribuida de manera uniforme sobre el disco, la carga total es directamente
el producto de la densidad de carga superficial y el área del disco:
El área del disco es simplemente S =πr2:
S =πr2 = π × (5×10-2 m)2 = 0.0079 m2
Sabiendo que σ = 1.2 ×
10-7 C/m2, la carga total guardada en el disco es:
Q=σ∙S = 1.2 ×
10-7 C/m2 × 0.0079 m2 = 9.5 ×
10-10 C.
Ejemplo 2
Distribución lineal de carga no uniforme
Se tiene un alambre de longitud L = 1.5 m, el cual tiene una densidad de carga dada por:
¿Cuál es la carga
total en el alambre?
Solución
La carga no está
distribuida uniformemente, sino que depende de la ubicación ‘x’ de cada punto
sobre el alambre. Si colocamos un sistema de referencia donde el alambre se
ubica sobre el eje horizontal (el eje x), y los tonos de gris
representan la carga, en x=0 será blanco (porque no hay carga) mientras que en x = 1.5
m la densidad de carga será máxima, por eso se ve en negro.
Un segmento arbitrario dx, que contiene una pequeña carga dq, ubicado en un lugar arbitrario del alambre, tendrá una densidad de carga intermedia. La figura servirá luego para calcular el campo eléctrico del alambre, pero eso queda para otro post.
Ahora vamos al cálculo de la carga total, que es muy simple:






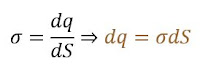





Buen trabajo!!
ResponderEliminar