Las ecuaciones irracionales con una incógnita, son aquellas en las cuales la incógnita aparece como parte del argumento de una raíz cuadrada, cúbica, cuarta, etc. Son frecuentes en ciencia e ingeniería, por ejemplo en:
- Geometría, para encontrar el radio ‘r’ de una esfera de volumen ‘V’:
- El movimiento
rectilíneo uniformemente variado, para encontrar la velocidad ‘v’
del móvil que parte del reposo, dadas la aceleración ‘a’ y la distancia
recorrida ‘d’:
- El teorema de Torricelli, según el cual la velocidad ‘v’ de salida de un fluido a
través de un orificio, es la misma que tendría si cayera libremente con
aceleración ‘g’ desde el nivel de la superficie del tanque, cuya profundidad es
‘h’:
- Oscilaciones: en el sistema masa-resorte, donde ‘m’ es la masa y el resorte
tiene una constante ‘k’, que cuantifica si es un resorte más o menos rígido, la
frecuencia de oscilación del sistema ‘ω’ viene dada por:
Solución de las ecuaciones irracionales
Para resolver ecuaciones irracionales, es necesario tomar en cuenta que la operación inversa que permite despejar la incógnita dentro de la raíz es la potenciación.
Si la incógnita está bajo una raíz
cuadrada, hay que pensar en elevar al cuadrado, si está bajo una raíz cúbica, se
eleva al cubo y así sucesivamente. De igual manera, las reglas que se utilizan
para resolver otros tipos de ecuaciones, en principio pueden utilizarse en
estas ecuaciones, por ejemplo, transponer términos, así como multiplicar y/
dividir por una misma cantidad a ambos lados de la igualdad, cuando sea
necesario.
No obstante, hay que advertir que, al
transformar la ecuación original, se obtiene un conjunto solución que puede no
coincidir en su totalidad con el conjunto solución de la ecuación original.
Soluciones extrañas
Al resolver por los métodos tradicionales
una ecuación irracional, puede que se presenten las llamadas soluciones
extrañas, (en algunos textos se las llama soluciones espurias), las
cuales surgen debido a las transformaciones algebraicas que se llevan a cabo
para obtener la ecuación equivalente, cuya resolución sea inmediata.
Durante la implementación de dichos
procedimientos, en ocasiones se pasa por alto el hecho de que:
No existen raíces de índice par para cantidades negativas.
Por lo tanto, al resolver la ecuación
equivalente, aparecen soluciones que no son válidas en la ecuación original. Estas
son, precisamente, las soluciones extrañas.
Para descartarlas, se verifican las
soluciones en la ecuación original, antes de darlas como válidas.
Los siguientes ejemplos ilustran todo lo
dicho.
Ejemplo 1
Resolver la ecuación:Solución
Elevando al cuadrado a ambos lados de la
igualdad, se obtiene:
Al sustituir este valor en la ecuación original, se obtiene una igualdad. Se deja al lector la tarea de verificarlo.
Ejemplo 2
Resolver la ecuación:
Solo x=10, al ser sustituida en la
ecuación original, produce una igualdad. Se deja al lector la tarea de
comprobarlo. Por lo tanto, la solución buscada es:
Ejemplo 3
Solución
Ejemplo 4
¿Cuál es el radio de una esfera cuyo
volumen es 33.493 cm3?



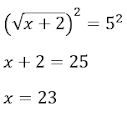




No hay comentarios:
Publicar un comentario