Presión y profundidad

La presión en un fluido ciertamente varía con la profundidad. Para determinar en que forma lo hace, consideremos una porción de fluido en total reposo, de espesor dy y área A, ubicada a una altura y respecto a un nivel de referencia. El resto del fluido que rodea a esta porción ejerce fuerzas por todos lados, pero la fuerza neta sobre ella es nula, ya que se encuentra en reposo.

Supongamos que se tiene un cubo de agua con aire por encima. La porción de fluido en reposo se representa de color rosa en la siguiente figura. Colocamos el 0 del nivel de referencia justo en la superficie libre del agua, la cara superior está a una profundidad y₁ y la inferior a y₂.

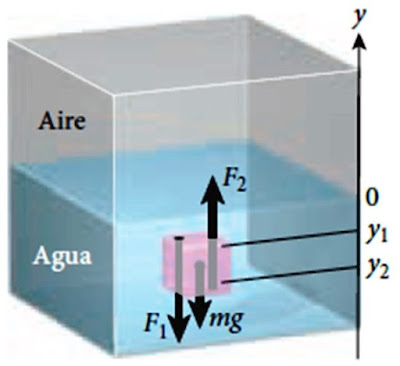Figura 1. Diagrama de cuerpo libre de una porción de agua. Fuente: Bauer, W. Física para ingeniería y ciencias.

Hay fuerzas actuando sobre esta pequeña porción de agua. Las horizontales se cancelan mutuamente y no están representadas en el diagrama. Para las fuerzas verticales tenemos, según el diagrama de cuerpo libre mostrado en la figura 1:

• El peso de la porción W, cuya magnitud es W = mg
• La fuerza que ejerce el resto del fluido hacia abajo F₁
• Y la que ejerce el resto del fluido hacia arriba F₂

La suma vectorial W + F₁ + F₂ debe anularse, por lo tanto, escogiendo hacia abajo como el sentido positivo:

∑F_y = 0

W + F₁ – F₂ = 0

En términos de la presión, las magnitudes de las fuerzas F₁ y F₂ pueden expresarse como:

F₁ = p₁ A

F₂ = p₂ A

El peso de la porción de fluido puede expresarse en términos de la densidad:

W = ρ_fluido V. g

Por lo tanto:

ρ_fluido V. g + p₁ A – p₂ A = 0

ρ_fluido V. g + (p₁  – p₂ )A = 0

Dado que p₂  – p₁ = Δp, tenemos:

ρ_fluido V. g - Δp A = 0

Pero el volumen  de la porción es el producto de la altura y₂ – y₁ = Δy de la misma, por el área A: V = A.Δy

ρ_fluido g (A. Δy). - Δp A = 0

Entonces:

ρ_fluido g. Δy - Δp = 0

Y finalmente:

Δp = ρ_fluido g. Δy

Tomando la coordenada y₁ sobre la superficie libre del fluido y llamando p_o a la presión allí, a una profundidad h, la presión viene dada por:

p = p_o + ρ_fluido g. h

La ecuación anterior se puede expresar en términos del peso específico del fluido γ _fluido = ρ_fluido g:

p = p_o + γ_fluido. h

Por lo tanto, la presión aumenta linealmente con la profundidad vertical (la coordenada horizontal no influye para nada, cualquier punto sobre la misma línea horizontal estará a una misma presión). Y en numerosas ocasiones (pero no siempre) la presión p_o corresponde a la presión atmosférica, cuando el recipiente está abierto al aire.

Figura 2. La presión bajo el mar aumenta con la profundidad. Fuente: Wikimedia Commons.

En el análisis anterior hemos considerado que la presión del fluido permanece constante, es decir, se trata de un fluido incompresible, una característica que sabemos se cumple aproximadamente en el caso de los líquidos como el agua de nuestro ejemplo. Sin embargo, en el caso de los gases es diferente, porque estos sí son compresibles fácilmente.

Ejemplo resuelto 1

¿Cuál es la presión en el fondo de una piscina de profundidad uniforme 2 m? Si el área de la piscina es 22 m x 8.5 m ¿cuál es la magnitud de la fuerza ejercida por el agua sobre el fondo?

Solución

La presión en el fondo se calcula mediante la ecuación:

p = p_o + ρ_fluido g. h

Donde p_o es la presión atmosférica cuyo valor es 101325 Pa. La densidad del agua dulce es de 1000 kg/ m³, la gravedad vale 9.8 m/s² y el enunciado dice que la profundidad de la piscina es de 2 m, por lo tanto:

p = 101325 + 1000 x 9.8 x 2  Pa = 120925 Pa.

En cuanto a la fuerza ejercida sobre el fondo, se puede calcular a partir de la definición de presión:

P = F/ A

El área del fondo es A = 22 m x 8.5 m = 187 m²

Entonces, la fuerza es:

F = P. A = 120925 Pa x 187 m² = 2.26 x 10⁷ N

Ejemplo resuelto 2

¿A qué profundidad hay que sumergirse en el mar para que la presión sea de 5 Mpa? La densidad del agua de mar es 1027 kg/m³.

Solución

Mediante:

p = p_o + ρ_fluido g. h

Se despeja la profundidad h:

h= (p - p_o )/( ρ_fluido g)

Se sustituyen los valores:

p_o = 101325 Pa; p = 5 Mpa = 5 x 10⁶ Pa ; ρ_fluido = 1027 kg/m³

h = (5 x 10⁶ – 101325) Pa / (1027 kg/m³ x 9,8 m/s²) = 486.7 m

Ejemplo resuelto 3

Un barril sin tapa contiene aceite hasta ¼ de su altura. Expuesto a una lluvia intensa, se llena de agua completamente sin que nada llegue a derramarse. Sabiendo que el barril tiene 1 m, hallar la presión en el fondo.

Dato: la densidad del aceite es 0.8 g/cm³

Solución

El agua ejerce una presión sobre el fondo y completó ¾ partes de la altura del barril, por lo tanto h_agua = 0,75 m. Por otra parte, al ser más densa que el aceite, queda en el fondo.

La capa de aceite queda arriba, a presión atmosférica y ocupando una capa de 0.25 m. Importante convertir la densidad del aceite a unidades del Sistema Internacional antes de sustituirla en alguna ecuación:

ρ_aceite = 800 kg/m³

La presión hasta esa profundidad es:

p = p_o + ρ_aceite g. h = 101325 Pa + 800 kg/m³ x 9.8 m/s² x 0.25 m = 103285 Pa

Por su parte, el agua ejerce la presión:

p = p_o + ρ_agua g. h = 103285 Pa + 1000 kg/m³ x 9.8 m/s² x 0.75 m = 110635 Pa

Si no se tomara  en cuenta la presión atmosférica, sino únicamente la presión que se debe a los fluidos en el interior del barril, esa sería: 110635 Pa - 101325 Pa = 9310  Pa.

Por F. Zapata