El par de fuerzas

 

Como el nombre lo indica, un par de fuerzas consiste en dos fuerzas no colineales, de la misma magnitud y dirección, pero sentidos opuestos, que al ser aplicado sobre un cuerpo, solamente es capaz de producirle rotación y no traslación.

Los pares de fuerzas o cuplas aparecen con frecuencia en la vida diaria, pues se requieren para accionar numerosos dispositivos. Además del volante de automóvil, que es un ejemplo muy típico y que analizaremos más adelante, el par de fuerzas aparece al aflojar una llanta con la llave de cruz, en el sacacorchos, los destornilladores y más.

El par de fuerzas actúa al utilizar la llave de cruz para aflojar las tuercas del neumático. Fuente: Ivan radic en Flickr.

Por ejemplo considérese el caso del volante que se muestra abajo, al cual se desea comunicar una rotación, para lo cual se le aplican dos fuerzas, en puntos diametralmente opuestos, es decir, no son fuerzas colineales. Ambas son verticales y de igual magnitud, pero tienen sentidos opuestos.

Estas fuerzas, llamadas F₁ y F₂, conforman un par de fuerzas, o simplemente un par. Sus puntos de aplicación están separados una distancia D, que en la figura es el diámetro del volante.

F₁ + F₂ = 0

Como es natural, su suma vectorial es nula, y el volante no se traslada, pero sí puede girar. En la disposición de fuerzas mostrada en la izquierda, el giro es antihorario, mientras que a la derecha, el giro es horario.

Para visualizarlo, se calcula el torque o momento resultante M_R, respecto al punto O, por ejemplo. Tanto las fuerzas como el vector de posición son perpendiculares, así que el momento resultante es perpendicular al plano de la pantalla, que sería la dirección del eje z.

La distancia entre el punto de aplicación de la fuerza y el punto O es el radio del volante, al cual se le denota R.

En la configuración de la izquierda, y siguiendo la regla de la mano derecha para el momento, resulta que el momento neto es positivo, por lo que el giro es antihorario, el cual es, por convención, positivo:

M_R = M₁ + M₂ = F₁ × r₁ + F₂ × r₂ = (F₁R + F₂R) k = 2FR k = FD k

Ya que F₁ = F₂ = F (las dos fuerzas tienen la misma magnitud, llamada F)

Mientras que en la configuración de la derecha, los momentos se dirigen hacia dentro de la pantalla:

M_R = M₁ + M₂ = (−F₁ × r₁ ) + (−F₂ × r₂ )= −(F₁R + F₂R) k = −2FR k = −FD k

En conclusión, la magnitud del momento producido por este par de fuerzas respecto al punto O es simplemente la magnitud de las fuerzas multiplicada por la distancia que las separa. Pero este resultado es válido para cualquier punto O arbitrario y un par de fuerzas cualesquiera, aplicadas sobre un cuerpo.

El momento de un par de fuerzas

En la siguiente la siguiente imagen hay un objeto arbitrario y una par de fuerzas, F y – F; el vector r se ha dibujado desde – F hasta F, el momento se calcula respecto al punto O, por lo que r_A es el vector desde el punto O hasta el punto A, que está sobre la línea de acción de – F.

El momento respecto al punto O es:

M_O = r_A × (−F) + r_B × F = ( −r_A + r_B ) × F = (r_B  − r_A ) × F

El triángulo azul muestra una suma de vectores:

r_A + r = r_B

Por lo tanto:

r = r_B − r_A

Y al sustituir queda:

M_O = r × F = M

Se puede prescindir del subíndice, ya que no depende del punto respecto al cual se calcula.

En cuanto a módulo, es:

M = r ∙ F∙ sen θ = F∙ (r∙sen θ)

Siendo θ el ángulo entre F y r. Haciendo:

d = r∙sen θ

Que es la distancia perpendicular entre las fuerzas, llamada brazo de palanca, la magnitud del momento es:

M = F ∙ d

El vector M resultante es perpendicular al plano al que pertenecen F y −F, y puede ir en sentido antihorario o en sentido horario. En el ejemplo que se muestra, el giro producido por este par ocurre en sentido antihorario (contrario a las manecillas del reloj) y está indicado por la flechita curva de color azul.

El vector M es un vector libre, ya que no depende del punto seleccionado para calcularlo. Esto significa que se pueden mover los puntos de aplicación A y B, sobre las respectivas líneas de acción de cada fuerza, sin que se modifique su efecto rotacional. Este resultado es importante.

Resumen

• La resultante de un par de fuerzas es nula, por lo tanto no produce traslación en el objeto sobre el que se aplica.
• El momento de un par de fuerzas nunca es nulo, entonces un par de fuerzas origina siempre una rotación.
• El momento del par no depende del punto respecto al cual se calcule.
• La dirección del momento es perpendicular al plano que contiene las fuerzas.
• El sentido del giro se determina con la regla de la mano derecha.

Ejemplos resueltos

Ejemplo 1

Calcular el momento producido por el par de fuerzas mostrado en la siguiente figura:

Solución

La magnitud del momento viene dada por:

M = F ∙ d = 50 kg-f × 16 m = 800 kg-f×m

Si el eje z entra o sale de la pantalla, y esta dirección está asociada con el vector unitario k, dado que el par produce una rotación en sentido horario (verificarlo con la regla de la mano derecha), entonces:

M = 800 kg-f×m (−k)

Ejemplo 2

Calcular el momento que produce el par mostrado sobre el rectángulo de dimensiones 10 m × 6 m.

Solución

Método 1

A través de M = F ∙ d se calcula la magnitud del momento, mientras que la dirección y el sentido se encuentran a partir de la regla de la mano derecha:

M = 20 kg-f × 10 m = 200 kg-f∙m

El momento está dirigido a lo largo del eje perpendicular a la pantalla, que es el eje z, y tiende a hacer girar el rectángulo en sentido horario, por lo tanto:

M = 200 kg-f×m (−k)

Método 2

Se elige un punto arbitrario respecto al cual calcular el momento, puede ser el origen del sistema de coordenadas O, ya que la una de las fuerzas está aplicada allí. Entonces el momento de esta fuerza es nulo y se ahorra el cálculo, quedando solo el momento de la otra fuerza por calcular.

Dicha fuerza es:

F = −20 kg-f j

Según la definición de momento, el cual es un producto cruz:

M = r × F = (10 i + 6 j) m × (−20 kg-f) j = 10×(−20) kg-f∙m (i×j) = −200 kg-f∙m k

Método 3

Se aplica:

M = r ∙ F∙ sen θ

Aplicando el teorema de Pitágoras:

Se sustituye todo esto en la magnitud del momento:

Dado que la fuerza y el vector de posición están en el plano xy, el momento es perpendicular a dicho plano, por lo tanto debe estar en el eje z y su tendencia es hacer girar el rectángulo en sentido horario. Por lo tanto:

M = −200 kg-f∙m k

Ejemplo 3

Sobre la palanca que se muestra en la figura se aplica un par de magnitud igual a 60 N. Calcular el momento producido por el par.

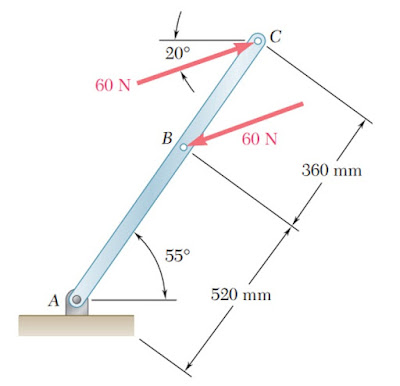Fuente: Estática. Beer-Johnston.

Solución

Como se deduce de los ejemplos anteriores, hay varias formas de resolver, puesto que el momento resultante no depende de la elección del punto respecto al cual se calcule.

La estrategia que se aplicará enseguida es la del método 1 del ejemplo anterior, es decir, encontrar el brazo de palanca y multiplicar por la magnitud de la fuerza, de esta forma se tendrá la magnitud del momento, el cual debe tener dirección entrante o saliente a la pantalla.

Para ello se usará el triángulo rectángulo de color morado de la figura, con la finalidad de encontrar el brazo de palanca d, más la ayuda de con la información suministrada en la figura.

El truco consiste en hallar alguno de los ángulos internos de dicho triángulo, cuya hipotenusa vale 360 mm. Del dibujo es fácil ver que el ángulo cuyo vértice es B, es 55º − 20º = 35º, entonces, el brazo de palanca d es:

d = 360 mm × sen 35º = 206.5 mm

Por lo tanto:

M = 60 N × 0.2065 m = 12.4 N∙m

Dado que las fuerzas están en el plano xy, el momento tiene dirección z, es decir, perpendicular al plano de la pantalla, y su sentido es horario, ya que tiende a rotar la barra en el sentido de las manecillas del reloj:

M = 12.4 N∙m (−k)

Se deja al lector como ejercicio resolver este problema de acuerdo a los métodos 2 y 3 del ejemplo anterior.