Existen varias versiones de este problema, pero todas comienzan cuando el rey Hierón de Siracusa, una colonia griega ubicada en la isla de Sicilia unos 300 años antes de Cristo, mandó a elaborar una corona nueva con un conocido orfebre de la ciudad.
Naturalmente, el soberano le entregó al orfebre una cantidad de oro suficiente para fabricar la corona.
Cuando el artesano le trajo al rey su corona nueva, de inmediato este comenzó a sospechar que el orfebre le había engañado, mezclando el oro con algún otro metal menos noble y más ligero, pero la corona le gustaba y no quería destruirla, así que… ¿cómo confirmaría sus sospechas sin dañarla?
Conociendo la fama de sabio que tenía Arquímedes (287-212 a.C.), Hierón le encargó la tarea de determinar si la corona era o no de puro, sin dañarla.
Para llevar a cabo la misión, el sabio tuvo que meditar largamente, hasta que un día, mientras tomaba un baño, se dio cuenta de que se sentía mucho más liviano cuando estaba metido en la tina que cuando estaba fuera de ella. Entonces salió corriendo desnudo por las calles de Siracusa, gritando eureka, que en griego significa lo encontré.
 |
| Arquímedes se dio cuenta de que se sentía más liviano cuando estaba sumergido en la bañera, ello se debe a que el agua ejerce una fuerza vertical que contrarresta el peso. Fuente: Wannapic. |
Respuesta
Son conocidas las densidades del oro y el agua:
- ρoro = 1.93 x 104 kg/m3 = 19300 kg/m3
- ρagua = 1.00 x 103 kg/m3 = 1000 kg/m3
Para decidir si la corona es de oro o no, hay que determinar su densidad y compararla con la densidad conocida del oro. Si son parecidas, seguramente la corona es de oro, pero si son muy diferentes, probablemente el orfebre haya fabricado la corona con alguna aleación de otros metales, normalmente con menor densidad, como la plata, por ejemplo.
La densidad es la relación existente entre la masa y el peso de un objeto:
La masa de la
corona se conoce rápidamente, pues Arquímedes la pesó en el aire:
W = Mg
El cálculo lleva a:
M = W/g = 22 N/9.8 m/s2 =
2.2449 kg
Falta conocer el volumen de la corona, para lo cual se la pesa sumergida en agua.
 |
| El peso aparente del objeto sumergido en agua en menor que el peso en el aire. Fuente: http://hyperphysics.phy-astr.gsu.edu/hbasees/pbuoy.html |
 |
| Diagrama de cuerpo libre de la corona del rey Hieron sumergida en agua. Fuente: F. Zapata. |
Las fuerzas que actúan sobre la corona estando sumergida son:
- Su peso W, dirigido verticalmente hacia abajo y ejercido por la Tierra.
- El empuje B, ejercido por el agua y dirigido verticalmente hacia arriba
- La tensión T en la cuerda que sujeta a la corona, también vertical y hacia arriba, y es equivalente al peso sumergido de la corona, o peso aparente.
Dado que las fuerzas son verticales y la corona está en equilibrio estático, al aplicar la segunda ley de Newton, queda:
∑ Fy = T + B – W = 0
Se deduce que:
B = W – T
Es decir, el empuje es igual a la diferencia entre el peso real (en aire) y el peso aparente (sumergido). Ahora bien, la magnitud de la fuerza del empuje viene dada por la ecuación:
B = ρagua ∙Vcorona ∙ g
Al sustituir esto en el despeje de B:
W – T = ρagua
∙Vcorona ∙ g
Y ya se puede despejar y calcular el volumen de la corona, ya que la tensión T equivale numéricamente al peso sumergido, el cual se conoce a partir del enunciado:
Conocido este
valor, se puede calcular la densidad de la corona ρcorona a ver si
coincide o al menos es lo bastante cercana a la del oro:
Sustituyendo en la densidad el valor M = 2.2449 kg previamente calculado:
ρcorona = 2.2449 kg / 0.0002041 m3 = 11000 kg/ m3
Como el
resultado es bastante menor que la densidad del oro, se deduce que el orfebre
seguramente engañó al rey, ya que la corona no puede ser de oro puro.
¿Y qué fue del orfebre deshonesto? Aparentemente fue ejecutado por tratar de robar al rey Hierón.
Por F. Zapata


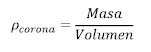
No hay comentarios:
Publicar un comentario