Enunciado del problema
Se tienen 3
cargas puntuales ubicadas en los vértices de un triángulo equilátero cuyo lado
mide L = 20 cm. Calcular el campo eléctrico que esta distribución de cargas
produce en el centro del triángulo, sabiendo que:
q1
= + 2.5 μC ; q2 = + 4.2 μC; q3 = −3.6 μC
Solución
Llamemos C al centro del triángulo. El vector campo eléctrico que una carga puntual produce en un punto dado, se calcula mediante la siguiente ecuación:
Donde q es el
valor de la carga, r es la distancia entre la carga y el punto donde se quiere
encontrar el potencial y k es la constante electrostática, que en unidades del
SI es:
k = 9 ×
109 N∙m2
/C2
El campo
eléctrico es una cantidad vectorial, que atiende al principio de superposición.
Es decir, el campo neto en un determinado punto, es la suma vectorial de los
campos producidos por cada una de las cargas:
Tratándose
de una figura altamente simétrica como el triángulo equilátero, la distancias r1,
r2 y r3 son las mismas. En este tipo de triángulo no es
difícil demostrar que su centro C está ubicado a una distancia h/3 por encima
de la base del triángulo, siendo h la altura del mismo.
El esquema
de los campos eléctricos, así como las respectivas distancias entre las cargas
y el centro C del triángulo aparecen dibujados en la siguiente figura:
Nótese que que
se ha dibujado un sistema de coordenadas cartesianas con el origen coincidiendo
con el punto C. Esto es muy importante, ya que el campo eléctrico es una
magnitud vectorial, por lo tanto, será necesario especificar cuidadosamente su
dirección y su sentido, no solamente su magnitud. Y esto se hace con la ayuda
de un sistema de coordenadas.
Importante: Al dibujar
el campo eléctrico, este es saliente a las cargas positivas y entrante a las
cargas negativas.
Adicionalmente,
se han dibujado también algunos ángulos que resultarán útiles más adelante, a
la hora de calcular los campos.
Paso
1: Cálculo de las distancias
De la figura
anterior, se observa de inmediato que:
r1
= h – h/3 = 2h/3
Como el
triángulo equilátero es simétrico, las distancias r2 y r3 son
iguales a r1. El valor de h necesario se calcula con trigonometría
elemental o el teorema de Pitágoras utilizando este triángulo rectángulo, que
la mitad del triángulo equilátero:
h = 20 cm × sen 60º = 17.3 cm
Por lo
tanto:
r1 = 2h/3 = (2×17.3 cm)/3 = 11.53 cm
Esta será la distancia a utilizar en los siguientes cálculos.
Paso 2:
Cálculo de los campos eléctricos
El campo producido por q1 apunta verticalmente hacia abajo (flecha roja), esta es la dirección del vector unitario −j:
En esta operación y en las que siguen, es preciso tener en cuenta que:
-Los
centímetros se pasan a metros multiplicando por 10-2, ya que el
valor de la constante electrostática k está en unidades del Sistema
Internacional SI.
-Asimismo, la magnitud de las cargas se multiplica por 10-6 para pasar de microcoulomb (μC) a coulomb (C) y trabajar en el Sistema Internacional.
-El campo
eléctrico es fuerza por unidad de carga, por lo tanto, la unidad en el SI es
N/C.
El campo
producido por q2 forma un ángulo de 60º respecto al eje y
positivo (flecha turquesa), por lo tanto, tiene componentes en las direcciones i
y j:
Por último,
el campo producido por q3 forma un ángulo de 60º respecto al eje
y negativo (flecha ocre), por lo tanto, tiene componentes en las direcciones
i y −j:
Paso 3: Cálculo del campo eléctrico neto






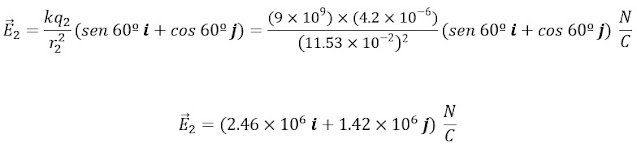


No hay comentarios:
Publicar un comentario