Frances Physics: Cómo calcular una derivada por definición (método de los 4 pasos)

La derivada de una función se define de manera algebraica a través de un límite, el cual representa la pendiente de la recta tangente a la curva en un punto dado:

Si el límite no existe, entonces simplemente la función no es derivable.

El método de los cuatro pasos describe la secuencia de pasos para encontrar algebraicamente la derivada de una función a través de su definición por límite, procurando minimizar los errores al momento de plantearla:

Paso 1

Calcular:

Paso 2

Encontrar:

Paso 3

Plantear el cociente:

Paso 4

Tomar el límite:

Es innegable que el procedimiento resulta a veces un tanto engorroso, sobre todo si la expresión algebraica de la función no es sencilla. Por este motivo, los matemáticos han deducido las reglas de derivación a partir de la definición, e incluso es posible derivar numéricamente.

No obstante, cuando se inicia en el tema del cálculo diferencial, el hecho de calcular la derivada por definición es muy útil para desarrollar una mejor intuición matemática del concepto. Por eso, al comienzo de los cursos, siempre se le pide a los estudiantes que encuentren algunas derivadas a través del límite.

Con algo de práctica no tiene que ser difícil, siempre que se sigan los pasos indicados y se opere con cuidado. El tema de la factorización es muy relevante aquí, así como las indeterminaciones de tipo 0/0 que se han estudiado previamente, por eso recomendamos revisar los posts dedicados a estos temas, cuyos enlaces aparecen a continuación:

https://www.todociencia.org/2023/11/factorizar-una-expresion-algebraica.html

https://www.todociencia.org/2023/11/racionalizacion.html

https://www.todociencia.org/2021/11/como-resolver-un-limite-de-la-forma-00.html

En todo caso, el resultado del límite, si existe, será la derivada de la función.

A continuación, algunos ejemplos que ilustran el método descrito para hallar derivadas por definición. En el primero, el límite es fácil de encontrar, pero, en los ejemplos 2 y 3, es un poco más engorroso, ya que requiere un buen manejo de productos notables, racionalización y simplificación de términos semejantes.

Ejemplo 1

Encontrar la derivada de la siguiente función mediante la definición por límite:

Solución

Paso 1

Paso 2

Paso 3

Paso 4

Es importante destacar que el límite es lo último que se lleva a cabo y solo cuando la expresión está totalmente simplificada. Esto es así para que el procedimiento de tomar el límite no se complique.

La derivada existe cuando “h” se cancela de tal forma que la indeterminación desaparece.

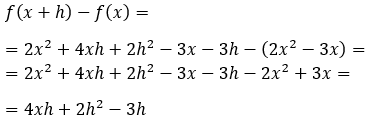
Ejemplo 2

Encontrar la derivada de la siguiente función mediante la definición por límite:

Solución

Paso 1

Paso 2

Paso 3

Paso 4

Este límite se resuelve mediante la racionalización del numerador, que consiste en multiplicar y dividir la expresión por el conjugado de dicho numerador.

Para una mejor comprensión, el conjugado se ha resaltado en otro color. El observador atento notará que el denominador de la expresión resultante no se trabaja, sino que se deja tal cual como está, con la esperanza de que, al final, la indeterminación desaparezca.

Puesto que la función es derivable, afortunadamente esto es lo que sucederá, no sin antes hacer un poco de trabajo algebraico:

En último lugar, proponemos un ejercicio que queda reservado a los más audaces, cuyo límite también se resuelve mediante racionalización del numerador, pero con más trabajo algebraico. Igual se deja la solución paso a paso: