Ejercicio 1
Velocidad media
 |
| Fuente: Pixnio. |
Solución
Ejercicio 2
Movimiento Rectilíneo Uniforme
Sabiendo que la luz del Sol tarda en llegar a la Tierra 8 minutos y 19 segundos. ¿Cuál es la distancia entre el Sol y la Tierra?
Solución
Se puede pensar en un rayo de luz que parte del Sol y recorre una distancia ‘d’ hasta llegar a la Tierra. Normalmente, a la velocidad de la luz se la denota con la letra ‘c’ y entonces se puede utilizar la ecuación:
d = c∙ t
Donde ‘t’ es el tiempo de viaje del rayo de luz. Sin embargo, antes de sustituir en la ecuación para determinar ‘d’, es necesario expresar todas las magnitudes en el mismo sistema de unidades. El kilómetro debe ser una unidad apropiada para la distancia entre la Tierra y el Sol, por lo que se expresará el tiempo de viaje en segundos:
t = 8 min y 19 s = 8×60 s + 19 s = 480 s + 19 s = 499 s
Entonces, efectuando la operación, se obtiene:
d = c∙ t = 300.000 km/s × 499 s = 149.700.000 km
Esta es la distancia media Tierra-Sol, pero para que sea más fácil de recordar, se suele redondear a 150 millones de kilómetros, que corresponde a una unidad astronómica, abreviada UA. De esta manera, la Tierra dista del Sol 1 UA, mientras que Marte, por ejemplo, está un poco más lejos, a 1.52 UA.
Ejercicio 3
Movimiento Rectilíneo Uniforme
El sonido se propaga en el aire aproximadamente a 340 𝑚/𝑠. ¿En cuánto tiempo se escuchará el estruendo del disparo de un cañón situado a 16 𝑘𝑚?
Solución
De la ecuación:
x = v∙t
Se despeja el tiempo:
Pero antes de sustituir, es preciso hacer que todas las magnitudes estén en el mismo sistema de unidades:
x = 16 km = 16×1000 m = 16000 m
Entonces:
Por lo tanto, el estampido del cañón se escucha al cabo de solo 47.06 segundos, es decir, algo menos de un minuto.
Ejercicio 4
Movimiento Rectilíneo Uniforme
¿Cuál es la ecuación de un móvil que se desplaza con velocidad constante 𝑣 = −2 𝑚/𝑠 si su posición inicial es 𝑥0 = 9 𝑚?
Solución
Se sustituyen los valores dados en el enunciado en la ecuación de movimiento:x(t) = 9 − 2t
Ejercicio 5
Movimiento Rectilíneo Uniforme
La siguiente gráfica muestra la posición versus el tiempo para los móviles 1 y 2 que se mueven a lo largo de la recta dada por el eje x.
A) ¿Qué tipo de movimiento tienen?
B) ¿Cuál de ellos tiene mayor velocidad?
C) ¿Qué representan los puntos de intersección con el eje vertical?
A) ¿Qué tipo de movimiento tienen?
B) ¿Cuál de ellos tiene mayor velocidad?
C) ¿Qué representan los puntos de intersección con el eje vertical?
Respuesta A
Ambos móviles tienen movimiento rectilíneo uniforme, ya que sus respectivas gráficas de posición versus tiempo son líneas rectas.
Respuesta B
El móvil 2 es el que tiene mayor velocidad, puesto que su pendiente es mayor.
Respuesta C
El punto de intersección con el eje vertical coincide en ambos casos, esto significa que los móviles tienen el mismo punto de partida. Además, ambos partieron en el instante t = 0,
Ejercicio 6
Movimiento Rectilíneo Uniforme
A continuación, se muestra la gráfica de dos móviles con movimiento rectilíneo uniforme. Calcular:
A) La velocidad de cada uno.
B) ¿Qué distancia los separa al cabo de 2 segundos? ¿Y al cabo de 4 segundos?
C) ¿Cuánto tarda el móvil 1 en llegar a x = 7m? ¿Y cuánto tarda el móvil 2 en llegar a esa misma posición?
Respuesta A
Dado que la velocidad equivale a la pendiente de la recta, viene dada por la fórmula:
Por lo tanto, hay que seleccionar dos puntos de cada recta, pero como ambas pasan por el punto (0,0), se puede tomar ese como el punto (t1, x1), quedando el punto (t2, x2) a elección.
Para el móvil 1
Se toma como (x2; t2) al punto (4s; 3m) y al sustituir en la fórmula, queda:
Para el móvil 2
El procedimiento es análogo, en este caso, se elige el punto (4s; 6m)
Por lo tanto, hay que seleccionar dos puntos de cada recta, pero como ambas pasan por el punto (0,0), se puede tomar ese como el punto (t1, x1), quedando el punto (t2, x2) a elección.
Para el móvil 1
Se toma como (x2; t2) al punto (4s; 3m) y al sustituir en la fórmula, queda:
Para el móvil 2
El procedimiento es análogo, en este caso, se elige el punto (4s; 6m)
Respuesta B
Las respuestas se obtienen leyendo el gráfico cuidadosamente. Es importante destacar que, en este gráfico, la posición se lee del eje vertical, mientras que el tiempo se lee en el eje horizontal.
Al cabo de t = 2 s, el móvil 1 se encuentra en x = 1.5 m, mientras que el móvil 2 está en x = 3 m, por lo tanto, están separados una distancia Δx = 3 m – 1.5 m = 1.5 m.
Mientras que, al cabo de t = 4 s, el móvil 1 está en x = 3m, y el móvil 2 está en x = 6 m, por lo tanto, están separados una distancia Δx = 6 m – 3 m = 3 m.
Las respuestas se obtienen leyendo el gráfico cuidadosamente. Es importante destacar que, en este gráfico, la posición se lee del eje vertical, mientras que el tiempo se lee en el eje horizontal.
Al cabo de t = 2 s, el móvil 1 se encuentra en x = 1.5 m, mientras que el móvil 2 está en x = 3 m, por lo tanto, están separados una distancia Δx = 3 m – 1.5 m = 1.5 m.
Mientras que, al cabo de t = 4 s, el móvil 1 está en x = 3m, y el móvil 2 está en x = 6 m, por lo tanto, están separados una distancia Δx = 6 m – 3 m = 3 m.
Respuesta C
Observando atentamente el gráfico, y ayudándose con las cuadrículas, se observa que el móvil 1 llega a x = 7 m aproximadamente al cabo de t = 9.25 s, mientras que el móvil 2, al ser más rápido, llegó allí al cabo de t = 4.5 s aproximadamente.
Observando atentamente el gráfico, y ayudándose con las cuadrículas, se observa que el móvil 1 llega a x = 7 m aproximadamente al cabo de t = 9.25 s, mientras que el móvil 2, al ser más rápido, llegó allí al cabo de t = 4.5 s aproximadamente.
Ejercicio 7
Movimiento Rectilíneo Uniforme
La siguiente es la gráfica velocidad tiempo de un móvil con movimiento rectilíneo uniforme, en unidades del Sistema Internacional. Determinar:
A) La velocidad del móvil
B) Distancia recorrida al cabo de t = 3s
C) Distancia recorrida entre t = 2 s y t = 6 s
La siguiente es la gráfica velocidad tiempo de un móvil con movimiento rectilíneo uniforme, en unidades del Sistema Internacional. Determinar:
A) La velocidad del móvil
B) Distancia recorrida al cabo de t = 3s
C) Distancia recorrida entre t = 2 s y t = 6 s
Respuesta A
Del gráfico puede leerse directamente que la velocidad del móvil es de 10 m/s.
Del gráfico puede leerse directamente que la velocidad del móvil es de 10 m/s.
Respuesta B
Respuesta C
Ejercicio 8
Problema con dos móviles
Solución
Ejercicio 9
Problema con dos móviles
Dos localidades A y B están separadas una distancia de 300 km. A las 10 a.m., parte de A un móvil a 60 km/h en dirección a B, y simultáneamente, desde la localidad B, parte otro móvil a 40 km/h dirigiéndose a la localidad A.
a) ¿A qué hora se encuentran?
b) ¿Y a qué distancia de A lo hacen?
c) ¿Cuánto tarda el móvil que parte de A en llegar hasta el poblado B?
d) ¿Qué tiempo demora el móvil que parte de B en llegar al pueblo A?
Solución a
Este es un ejercicio típico, para el que conviene hacer un diagrama de la situación:
A la izquierda tenemos el pueblo A y a la derecha el pueblo B, separados por una carretera recta de dos sentidos y longitud igual a 300 km. Ambos móviles se desplazan sobre ella llevando un movimiento rectilíneo uniforme, puesto que el enunciado informa que sus velocidades se mantienen constantes.
Se verifica igualmente que las distancias y el tiempo están dados respectivamente en kilómetros y en horas, de no ser así, es necesario convertir todo a las mismas unidades.
Otro detalle importante es que los dos parten simultáneamente, por lo tanto, el tiempo ‘t’ es el mismo para los dos móviles, pero como se mueven en sentidos contrarios, la velocidad de uno de ellos se considera positiva, y para distinguirlo del otro, a este se le asignará velocidad negativa.
Dicho esto, se toma un sistema de referencia, y se selecciona el origen en algún lugar, por ejemplo, en A, entonces B se ubica en x = 300 km.
Ya se puede escribir la ecuación de movimiento para cada uno:
Móvil A
xA(t) = x0 + v∙t
Con x0 = 0, y vA = 60 km/h, por lo tanto:
xA(t) = 60∙t
Móvil B
xB(t) = x0 + v∙t
Con x0 = 300 km, y vA = −40 km/h, entonces:
xB(t) = 300 − 40∙t
El siguiente paso es igualar las dos ecuaciones:
60∙t = 300 − 40∙t
(60 + 40) ∙t = 300
t = 300/100 = 3 h
Si los móviles partieron al mismo tiempo a las 10 am, se encontrarán 3 horas más tarde, a la 1 pm.
Solución b
Para determinar la distancia del punto de encuentro al pueblo A, se sustituye x = 3 h en la respectiva ecuación de posición:
xA(t) = 60∙t = 60 km/ h∙ 3 h = 180 km
Los resultados se pueden verificar rápidamente construyendo la gráfica de la posición versus el tiempo para ambos móviles mediante alguna calculadora gráfica online como Desmos o Geogebra. Ambos recursos son gratuitos y fáciles de usar, por lo que son muy recomendables para verificar que los valores obtenidos son correctos.
Simplemente se colocan en las respectivas casillas las funciones de posición de cada móvil y la calculadora hace el resto. Cuando se grafican las respectivas posiciones sobre un mismo plano de coordenadas, con la posición en el eje vertical y el tiempo en el eje horizontal, el punto de encuentro será la intersección de las curvas.
Para el ejemplo propuesto, aquí se muestran las rectas que corresponden a los dos móviles, en rojo el móvil que parte de A, y en azul para el que parte de B. Nótese que la pendiente (que equivale a la velocidad) del primero es positiva, mientras que la del segundo es negativa.
El graficador online hace el cálculo de la intersección, que ocurre en el punto marcado en verde, cuyas coordenadas son t = 3 horas, x = 180 kilómetros. Esto coincide con los cálculos hechos más arriba.
Solución c
Solución d
Ejercicio 10
Problema con dos móviles
Un auto pasa por un punto de la carretera a una velocidad de 20 m/s y 10 segundos más tarde, pasa por el mismo lugar una patrulla de la policía que lo va persiguiendo a una velocidad de 30 m/s. Si ambos móviles mantienen todo el tiempo la misma velocidad, encontrar a qué distancia del punto en cuestión se encuentran el conductor y la patrulla, y al cabo de cuánto tiempo se produce el encuentro.
Solución
Este problema trata de dos móviles en persecución, pero que no pasan al mismo tiempo por el punto de referencia.
Lo primero que se debe hacer es determinar el tipo de movimiento de cada móvil, porque de esta manera se podrá elegir la ecuación más conveniente. El enunciado afirma que los móviles mantienen sus velocidades constantes, por lo tanto, el movimiento de cada uno es MRU, es decir, movimiento rectilíneo uniforme.
Enseguida se escoge un punto de referencia, el cual será ese punto de la vía al que hace referencia el enunciado.
A dicho punto se le asigna la coordenada x = 0 m, pero como los móviles no pasan al mismo tiempo por ese punto, podemos decir que el automovilista pasa por allí justo cuando se comienza a estudiar el movimiento, es decir, en t = 0 segundos. Por su parte, la patrulla pasa con 10 segundos de retraso.
Si el automovilista es el móvil 1, y t1 es su tiempo, podemos decir que t1 = t, tomándolo a él como referencia. Entonces t2 es el tiempo de la patrulla y t2 = t−10 segundos, ya que la patrulla siempre tiene retraso de 10 segundos (el signo negativo antepuesto a 10 segundos da cuenta de ese retardo).
Tomando en consideración todo lo antes dicho, se parte de la ecuación de movimiento para el MRU:
x(t) = x0 + v∙t
Y se adapta a cada móvil:
Móvil 1: el automovilista
x1(t) = x0 + v∙t
Con x0 = 0, ya que todo el movimiento comienza a observarse en ese punto que menciona el enunciado, al cual se le ha dado el valor de 0 m. Por lo tanto:
x1(t) = 20∙t
Móvil 2: la patrulla
x2(t) = 30∙(t −10)
Ahora se igualan ambas ecuaciones:
x1(t) = x2(t)
Lo que conduce a:
20∙t = 30∙(t−10)
20∙t = 30∙t −300
−10∙t = −300
t = 30 s
Se concluye que el auto y la patrulla se encuentran al cabo de 30 s, luego de pasar por el punto de referencia. Ahora, para saber a cuántos metros de dicho punto se produce el encuentro, basta sustituir este tiempo en cualquiera de las ecuaciones del movimiento, por ejemplo, en x1:
x1(t) = 20∙t = 20 m/ s ∙ 30 s = 600 m
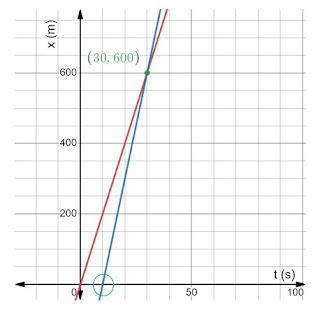
Es muy sencillo verificar estos resultados mediante la gráfica de la posición versus el tiempo para ambos móviles:
La gráfica correspondiente al móvil 1, el automovilista, se representa en rojo, mientras que la de la patrulla se dibujó en azul. Obsérvese que la recta del automovilista pasa por el origen, pero la de la patrulla parte de t = 10 segundos, como se señala en el círculo verde.
El punto de intersección es (30 s, 600 m), lo cual coincide con los cálculos previos.
Ejercicio 11
Problema con tres móviles
Un camión que viaja a 30 millas/h pasa de largo un semáforo en rojo en una avenida larga y recta. Mientras tanto, un automovilista que esperaba tranquilamente, al verse rebasado por el camión, asume que la luz ha cambiado y arranca con aceleración constante de 12 pies/seg 2. Dos segundos después, un oficial en motocicleta oculto en la intersección, sale del reposo con una aceleración constante y desconocida.
Si el oficial desea atrapar a ambos infractores, ¿cuál debe ser el valor de su aceleración para llegar al automovilista justo cuando está rebasando al camión?
Solución
Aquí tenemos tres móviles, aunque por el momento basta con preocuparse por los dos primeros: el camión C, cuyo movimiento es rectilíneo uniforme, y el automovilista A, que tiene movimiento rectilíneo uniformemente acelerado.
Todo comienza en el semáforo, cuya ubicación será x = 0, y el tiempo t= 0 s es aquel en el cual el auto es rebasado por el camión. Las unidades serán pies y segundos, por lo tanto, hay que convertir la velocidad del camión:
vC = 30 millas/h = 40 pies/s
La siguiente tabla es de utilidad para organizar la información que ofrece el enunciado:
Móvil C: el camión
xC(t) = x0 + v∙t
xC(t) = 40∙t
Móvil A: el automovilista
xA(t) = x0 + v0∙t+ ½ aAt2
Con v0 = 0 ya que parte del reposo y aA = 12 pies/seg 2, según dice el enunciado:
xA(t) = ½ 12t2 = xA(t) = 6t2
En seguida, se plantea la igualdad en ambas:
xC(t) = xA(t)
40∙t = 6t2
Lo cual conduce a:
6t = 40 → t = 6.7 s
La posición del encuentro ocurre en:
xC(t) = 40∙t = 40∙6.7 pies = 266.7 pies
Si se prefiere, se puede calcular la posición del encuentro a través de la ecuación del automovilista. Normalmente aparecen pequeñas diferencias en el resultado, debido al redondeo en las operaciones.
Los resultados se verifican con ayuda de una calculadora gráfica:
El móvil azul se representa en color azul y su gráfica es una parábola, mientras que el camión va en rojo y su gráfica es una recta. Nótese que hay dos intersecciones: (0,0) que se produce cuando se encuentran delante del semáforo, y la que ocurre posteriormente, en (6.7; 266,7). Tras eso, los móviles no vuelven a encontrarse de nuevo, si mantienen el mismo movimiento.
Ahora vamos a introducir al tercer móvil, el móvil P o patrulla, cuyo movimiento es rectilíneo uniformemente acelerado, la cual parte del reposo (v0) en la intersección y con 2 segundos de retardo. Entonces su ecuación es:
Móvil P: la patrulla
xP(t) = ½ aP(t−2)2
Como la patrulla intercepta a los otros dos, se deben encontrar en xP = 266.7 pies y t = 6.7 s, con estos valores:
266.7 = ½ aP(6.7−2)2 = ½ aP(4.7)2 = 11.045 aP
Por lo tanto:
aP = 24.1467 pies/s2
Veamos cómo quedan las tres gráficas superpuestas, porque a partir de ella se encontrarán algunos detalles interesantes.
Si todos los cálculos son correctos, las tres gráficas deberían interceptarse todas en el punto en cuestión.
Pero antes, hay que construir la ecuación para la patrulla con ayuda de este resultado:
xP(t) = ½ aP(t−2)2 = ½ ×24.1467× (t−2)2 = 12.0733(t−2)2
Ahora se ha agregado la curva correspondiente a la patrulla, en color verde:
Se observa que la gráfica de este tercer móvil también es una parábola, lo cual era de esperar, ya que su movimiento es rectilíneo uniformemente acelerado, al igual que el del automovilista, pero con diferente aceleración y además, su vértice está desplazado t = 2 segundos a la derecha, puesto que partió con retardo.
Lo siguiente es que la curva verde intercepta a las otras dos simultáneamente en el mismo punto calculado antes, por lo cual respiramos tranquilos, sabiendo que los resultados son correctos.
Pero además corta a las otras dos en distintos instantes, ambos previos al encuentro final, lo cual significa que la patrulla los rebasó por separado antes de encontrárselos a los dos.
Al camión lo rebasó al cabo de t = 0.595 segundos, mientras que al automovilista lo hizo luego de t = 1.173 segundos. Estos resultados se obtuvieron de la gráfica, pero se pueden confirma haciendo las intersecciones de la patrulla y el camión, y la patrulla con el automovilista, por separado.
Es decir, hay que plantear y resolver estas ecuaciones:
xP(t) = xC(t)
Y
Ejercicio 12
Movimiento Rectilíneo Uniformemente Variado
Se tiene el gráfico de la velocidad en función del tiempo para un móvil, que se muestra en la siguiente figura:
Partiendo del gráfico, responder las siguientes preguntas:
a) ¿Cuál es la velocidad inicial del móvil?
b) ¿Cuánto vale la velocidad máxima?
c) ¿En qué instante, o instantes se detiene el móvil?
d) Describir con detalle cada tipo de movimiento que ejecuta este móvil
e) Calcular la aceleración del móvil en cada tramo del movimiento
f) Construir la gráfica aceleración versus tiempo.
g) ¿Qué distancia recorre el móvil entre t = 0 s y t = 15 s?
h) ¿Cuál es la distancia total recorrida por el móvil?
Se tiene el gráfico de la velocidad en función del tiempo para un móvil, que se muestra en la siguiente figura:
Partiendo del gráfico, responder las siguientes preguntas:
Solución a
Solución b
Solución c
Solución d
En la gráfica se describe el movimiento durante un lapso de tiempo de 30 segundos, durante los cuales el móvil se mueve sobre una línea recta, de la siguiente manera:
I) Entre t = 0 y t = 10 s, el movimiento es rectilíneo uniforme MRU. Lo sabemos porque la velocidad es constante en este intervalo de tiempo e igual a −20 m/s.
II) Desde t = 10 s hasta t = 20 s, el movimiento es rectilíneo uniformemente acelerado MRUA, es decir, la aceleración es constante y positiva. Esto se conoce porque la gráfica es una recta de pendiente positiva.
III) Desde t = 20 s hasta t = 30 s, el movimiento es rectilíneo uniformemente retardado MRUR, dado que la gráfica en este intervalo de tiempo es una recta de pendiente negativa.
En la gráfica se describe el movimiento durante un lapso de tiempo de 30 segundos, durante los cuales el móvil se mueve sobre una línea recta, de la siguiente manera:
I) Entre t = 0 y t = 10 s, el movimiento es rectilíneo uniforme MRU. Lo sabemos porque la velocidad es constante en este intervalo de tiempo e igual a −20 m/s.
II) Desde t = 10 s hasta t = 20 s, el movimiento es rectilíneo uniformemente acelerado MRUA, es decir, la aceleración es constante y positiva. Esto se conoce porque la gráfica es una recta de pendiente positiva.
III) Desde t = 20 s hasta t = 30 s, el movimiento es rectilíneo uniformemente retardado MRUR, dado que la gráfica en este intervalo de tiempo es una recta de pendiente negativa.
Solución e
El movimiento consta de tres tramos:
I) La aceleración en el primer tramo, entre t = 0 s y t = 10 s es nula, ya que allí la velocidad es constante, como se dijo anteriormente. Por lo tanto:
a1 = 0 m/s2
II) El segundo tramo va desde t = 10 s hasta t = 20 s y la aceleración es la pendiente del segmento de recta. Para calcularla se necesitan dos puntos cualesquiera que pertenezcan a este segmento, por ejemplo (10 s, -20 m/s) y (15 s, 0 m/s), pero se puede tomar cualquier otra pareja de puntos, siempre y cuando pertenezcan al segmento. Entonces se calcula la pendiente de la recta como:
III) En el tercer segmento se espera una aceleración negativa, para calcularla se toman los puntos (25 s, 0 m/s) y (30 s, −20 m/s), o cualquier otro par que pertenezca al segmento en cuestión:
Solución f
La gráfica de la aceleración en función del tiempo se construye con los tres valores obtenidos anteriormente. Se puede hacer a mano, en papel milimetrado, o con un software online, como Desmos o Geogebra. En cualquier caso, se trata de una función por partes, que consta de tres segmentos, como se puede apreciar en la figura:
La gráfica de la aceleración en función del tiempo se construye con los tres valores obtenidos anteriormente. Se puede hacer a mano, en papel milimetrado, o con un software online, como Desmos o Geogebra. En cualquier caso, se trata de una función por partes, que consta de tres segmentos, como se puede apreciar en la figura:
Solución g
La distancia recorrida por el móvil equivale numéricamente al área comprendida entre la gráfica y el eje horizontal, por ejemplo, para el intervalo de tiempo entre t = 0 s y t = 15 s, es el área del trapecio sombreado en azul:
El área del trapecio viene dada por la fórmula:
Donde B es la longitud de la base mayor, b es la longitud de la base menor y h es la altura. Hay que precisar que estos valores son positivos siempre, puesto que se trata de las longitudes de los lados de la figura. En otras palabras, la equivalencia entre distancia y área del trapecio es solamente numérica.
Así, en el ejemplo mostrado:
B = 15 s; b = 10 s; h = 20 m/s
Con estos valores, la distancia recorrida por el móvil en el intervalo propuesto es:
También se hubiera podido dividir el trapecio en dos figuras, un rectángulo y un triángulo, calculando el área de cada uno por separado y luego sumando los resultados.
La distancia recorrida por el móvil equivale numéricamente al área comprendida entre la gráfica y el eje horizontal, por ejemplo, para el intervalo de tiempo entre t = 0 s y t = 15 s, es el área del trapecio sombreado en azul:
El área del trapecio viene dada por la fórmula:
Donde B es la longitud de la base mayor, b es la longitud de la base menor y h es la altura. Hay que precisar que estos valores son positivos siempre, puesto que se trata de las longitudes de los lados de la figura. En otras palabras, la equivalencia entre distancia y área del trapecio es solamente numérica.
Así, en el ejemplo mostrado:
B = 15 s; b = 10 s; h = 20 m/s
Con estos valores, la distancia recorrida por el móvil en el intervalo propuesto es:
También se hubiera podido dividir el trapecio en dos figuras, un rectángulo y un triángulo, calculando el área de cada uno por separado y luego sumando los resultados.
Solución h
La distancia total recorrida por el móvil se calcula a través de la gráfica sumando todas las áreas comprendidas entre la gráfica y el eje horizontal, ya sea por encima del eje o por debajo. En este ejemplo es muy sencillo, ya que dichas áreas corresponden a figuras geométricas muy conocidas, como rectángulos, triángulos y trapecios. De no ser así, sería necesario calcular una integral para conocer el área.
Del inciso anterior ya se tiene la distancia recorrida por el móvil entre t = 0 s y t = 15 s, la cual es:
d1 = 250 m
Quedan por calcular las distancias entre t = 15 s y t = 25 s (triángulo rosado), y luego desde t = 25 s hasta t = 30 s (triángulo verde):
El área de un triángulo es:
Donde b es la base y h es la altura, que en el ejemplo del triángulo rosado corresponden a:
b = (25 – 15 s) = 10 s
h= 20 m/s
Con estos valores, el área resultante es:
La distancia total recorrida por el móvil se calcula a través de la gráfica sumando todas las áreas comprendidas entre la gráfica y el eje horizontal, ya sea por encima del eje o por debajo. En este ejemplo es muy sencillo, ya que dichas áreas corresponden a figuras geométricas muy conocidas, como rectángulos, triángulos y trapecios. De no ser así, sería necesario calcular una integral para conocer el área.
Del inciso anterior ya se tiene la distancia recorrida por el móvil entre t = 0 s y t = 15 s, la cual es:
d1 = 250 m
Quedan por calcular las distancias entre t = 15 s y t = 25 s (triángulo rosado), y luego desde t = 25 s hasta t = 30 s (triángulo verde):
El área de un triángulo es:
Donde b es la base y h es la altura, que en el ejemplo del triángulo rosado corresponden a:
b = (25 – 15 s) = 10 s
h= 20 m/s
Ejercicio 13
Movimientos verticales bajo la acción de la gravedad
Se lanza una piedra hacia arriba, desde el nivel del suelo, con una velocidad inicial de 10.0 m/s.a) ¿Cuál es la velocidad de la piedra después de 0.50 s?b) ¿A qué altura sobre el nivel del suelo está la piedra después de 0.50 s?
Solución a
v(t) = vo – gt
v(0.5) = 10.0 – 9.8 x 0.5 m/s = 5.1 m/s
Solución b
Tomaremos yo = 0
y(t) = vo t - ½gt2
Por lo tanto:
y(0.5) = 10.0 x 0.5 - ½ x 9.5 x 0.52 m = 3.8 m
Solución b
Ejercicio 14
Movimientos verticales bajo la acción de la gravedad
Se lanza una piedra hacia abajo con una velocidad inicial de 10.0 m/s. La aceleración de la piedra es constante y tiene el valor de la aceleración en caída libre, 9.81 m/s2. ¿Cuál es la velocidad de la piedra después de 0.500 s?
Solución
v(t) = vo – gt = -10.0 – 9.81 x 0. 500 m/s = -14.905 m/s
v(t) = vo – gt = -10.0 – 9.81 x 0. 500 m/s = -14.905 m/s
Ejercicio 15
Movimientos verticales bajo la acción de la gravedad y dos móviles
Una niña arroja una moneda al pozo de los deseos, la cual cae una distancia de 7.00 m antes de golpear el agua. Si la rapidez del sonido es 343 m/s, ¿cuánto tiempo transcurre antes de que la niña escuche la moneda chocar contra el agua?
Solución
En este problema hay dos móviles, uno es la moneda, que tiene caída libre y el otro es el sonido, que tiene rapidez constante. Tanto la moneda como el sonido recorren 7.00 metros, la moneda lo hace mientras cae y el sonido lo hace justo después que la moneda impacta contra el agua.
Trabajaremos con g = 9.8 m/s2
(1) ysonido = 343.tsonido
(2) ymoneda = ½ gt2 moneda = 4.9 t2 moneda
El tiempo que tarda la niña en escuchar el sonido de la moneda golpeando al agua es la suma del tiempo que la moneda tarda en caer, más el tiempo que el sonido demora en alcanzar el oído de la niña:
(2) ymoneda = ½ gt2 moneda = 4.9 t2 moneda
ttotal = tsonido + tmoneda
De la ecuación (1) despejamos y calculamos el tiempo que tarda el sonido en subir la distancia de 7.00 m:
343.tsonido = 7
tsonido = (7÷343) s = 0.02 s
Y de la ecuación (2) se despeja el tiempo que tarda en caer la moneda, la misma distancia de 7.00 m:
4.9 t2 moneda = 7
tmoneda = √ (7÷4.9) s = 1.20 s
Finalmente la suma de ambos tiempos es:
ttotal = 0.02 + 1.20 s = 1.22 s
Este es el tiempo que tarda desde que la niña deja caer la moneda hasta que escucha el sonido proveniente del choque contra el agua.




























No hay comentarios:
Publicar un comentario