La racionalización consiste en reescribir una expresión fraccionaria que contenga radicales, de tal forma que estos no aparezcan en el numerador o el denominador, según sea el caso. Lo más usual es racionalizar los denominadores, lo cual facilita en muchos casos las operaciones con fracciones, como suma y resta, ya que es preferible operar cuando los denominadores son enteros (al menos en forma manual).
 |
| La ventaja de racionalizar denominadores es que resulta más sencillo operar cuando los denominadores son números enteros. Fuente: F. Zapata. |
Por último, la expresión se simplifica y queda lista para operar con ella.
En la práctica, se presentan denominadores de diversas formas algebraicas, de los cuales se describen a continuación los casos más usuales:
1) Denominador de la forma:
Este es el caso más sencillo, en el cual el
factor de racionalización es √a:
Ejemplo
Racionalizar el denominador de la expresión:
Solución
Ejemplo
Racionalizar el denominador de la expresión:
Solución
El factor de racionalización es:
Entonces:
2) Denominador de la forma:
Para este tipo de expresiones, el factor de racionalización es:
Por lo tanto:
Ejemplo
Racionalizar el denominador de la expresión:
Solución
Identificando en el factor de racionalización anterior, resulta:
a= x; m = 2 y n = 5
De allí que:
3) Denominador de la forma:
Si el denominador es un binomio que contiene radical,
hay que multiplicar numerador y denominador por el conjugado del denominador:
Ejemplo
Racionalizar el denominador de la expresión:
Solución
Ejemplo
Racionalizar el denominador de:
Solución
4) Denominador de la forma:
Al operar con este factor de racionalización, el denominador se convierte en:
Ejemplo
Racionalizar el denominador de:
Solución
a = 2, b = 3 y el signo en el denominador es negativo:
Ejemplo
Racionalizar el numerador de:
Solución
Para este ejercicio se escoge el producto notable con signo positivo en el binomio de raíces cúbicas, con a = x y b = 2, por lo que resulta:
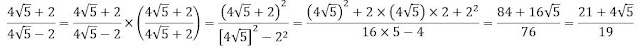
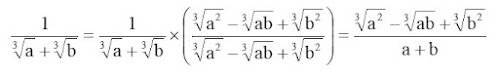
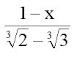
No hay comentarios:
Publicar un comentario