Los límites de una función matemática permiten evaluar el comportamiento de una función cuando la variable independiente se acerca a un valor específico x=c. De esta manera es posible averiguar, por ejemplo, si la función tiende a un valor finito o si, por el contrario, crece o decrece sin medida.
Los límites, en principio, se pueden clasificar en dos grandes grupos:
- Determinados
- Indeterminados
Un límite es determinado si al evaluar la función de acuerdo al valor al que se
hace tender la variable, se obtiene un valor definido. Un buen ejemplo está en
los límites de una función polinómica, cuyo dominio es el conjunto de los
números reales. En ese caso, el límite se obtiene por sustitución directa y da
como resultado un valor finito que coincide con el valor de la función en ese
punto.
Ejemplo 1
Calcular:
Límites indeterminados
Si al evaluar el límite se produce una
operación que no puede llevarse a cabo debido a que no está definida
matemáticamente, se dice que se ha producido una indeterminación.
Esto no significa necesariamente que el límite
no existe, ya que existen procedimientos algebraicos mediante los cuales es
posible hacer que la indeterminación desaparezca.
Ejemplo 2
Calcular, si existe:
Solución
Al intentar evaluar este límite por
sustitución directa, nos encontramos con que:
No obstante, factorizando el numerador,
el límite se puede calcular sin problema, pues la indeterminación desaparece
mediante este procedimiento:
En el caso de los límites con
indeterminación 0/0, la factorización busca precisamente eliminar el factor que
la origina, que en el caso anterior era x+2.
Factorizar no es la única estrategia
posible, ya que existen otras técnicas algebraicas como racionalización y
cambios de variable, por mencionar algunas. A veces pueden ser necesarias
técnicas más avanzadas de cálculo u otras ramas de las matemáticas. Además, hay
que resignarse al hecho de que algunos límites pueden simplemente no existir.
Nótese también que, aunque en este
ejemplo se obtuvo un valor determinado como límite, este no coincide con el
valor de la función en x = ─2, simplemente porque x = ─2 no pertenece al dominio de la función, ya que anula el denominador.
A pesar de todo, el límite existe en ese punto.
Según el valor del límite, hay otras posibilidades de clasificación. En tal sentido, se presentan los siguientes tipos:
- Límites finitos, si el límite de la función tiene un valor L.
- Límites infinitos, si el límite de la función resulta +∞ o ─∞.
Asimismo, se puede hacer tender a la variable a un valor puntual, como se ha hecho en casos anteriores, o bien al infinito. En tal caso, la variable puede ser:
- Finita, si x tiende a un valor finito L.
- Infinita, cuando x tiende a +∞ o ─∞.
Combinando todas las posibilidades descritas se obtiene:
Ejemplo 3
Solución
Si se intenta una sustitución directa se llega
la indeterminación 1/0, la cual no es posible evadir. Se dice, pues, que el
límite de la función cuando x tiende a 0 no existe.
Sin embargo, es interesante saber lo que
sucede con la función en las cercanías de x = 0, bien sea por la izquierda o
por la derecha, es decir, conocer los límites laterales de la función
cuando x tiende a 0.
Tomando valores ligeramente inferiores a
0, como por ejemplo -0.0001, -0.0000001…, etc., se observa que la función toma
valores positivos muy grandes.
Acercándonos a x = 0 con valores ligeramente mayores a cero, el
resultado nuevamente es un número positivo muy grande, por lo tanto, el límite
por la derecha de la función cuando x tiende a 0 es:
Como los límites laterales conducen siempre a números positivos indefinidamente grandes (+∞), entonces se concluye que:
Lo podemos comprobar a través de la gráfica de la función:
Ejemplo 4
Hallar, si existe, el siguiente límite:
Solución
Se dice entonces que
la recta y=1 es una asíntota horizontal de la función.
Al comportamiento de
la función cuando la variable toma valores muy grandes o muy pequeños se le
denomina comportamiento asintótico.
Esto es interesante, porque si la función describe algún fenómeno en función del tiempo, como una velocidad o el crecimiento de una población, conocer el comportamiento asintótico permitiría conocer la tendencia a largo plazo y, en consecuencia, planificar alguna acción o tomar una decisión.
Ejemplo 5
Solución
Acudiendo a la gráfica de la función que se muestra
ejemplo 3, es fácil ver que cuando la variable toma valores muy grandes, la
función tiende a 0. Tiene sentido, pues al dividir 1 entre un número muy grande
y elevado al cuadrado, el resultado debe ser muy pequeño. Por lo tanto:
Ejemplo 6
Una población crece según la siguiente función:
Donde t es el número de años transcurridos
desde 2010.
a) ¿Cuál era la población inicial?
b) ¿A cuánto asciende la población actual?
c) ¿Qué sucederá a largo plazo con la población?
Solución a
f(0)=1000
La población inicial era de 1000 individuos.
Actualmente, la población asciende a 2448
individuos (se redondea el resultado al entero más cercano)
Solución c
Podemos determinar la tendencia de la
función cuando x toma valores muy grandes a través de la gráfica, concluyendo
que tras un largo tiempo, la población alcanzará un valor límite de 2500
individuos. En otras palabras, la población se estabilizará.













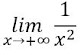





No hay comentarios:
Publicar un comentario