Cuando sobre un cuerpo actúan fuerzas que modifican su energía,
se dice que tales fuerzas hacen trabajo mecánico sobre el objeto. Esta magnitud física, de carácter escalar, relaciona a la fuerza con el desplazamiento del objeto. No todas las fuerzas favorecen un determinado desplazamiento.
La gravedad y
el roce cinético son ejemplos de fuerzas que hacen trabajo mecánico sobre un objeto en movimiento. En la caída libre por ejemplo, la gravedad hace que el
objeto aumente su velocidad a medida que cae. El roce, en cambio, frena a los móviles.
 |
| Figura 1. Cuando el constructor salta, la gravedad hace trabajo sobre él. Fuente: Pixabay. |
La normal, por su parte, es una fuerza que parece no
intervenir cuando un objeto se mueve. Ella simplemente actúa como soporte, pero
no le agrega velocidad a los objetos, ni la reduce. Entonces, como la normal
no favorece al movimiento, pero tampoco se opone, decimos que no hace trabajo
sobre el móvil.
Para calcular el trabajo que hace una fuerza sobre un objeto, es necesario saber cómo está aplicada ella en relación con el desplazamiento. Por eso, en Física, el trabajo se define como:
El producto escalar entre los vectores fuerza F y desplazamiento s.
Trabajo hecho por una fuerza
constante
Cuando la fuerza es constante, el trabajo, al que llamaremos
W, se define, como hemos dicho ya, mediante el producto escalar entre el vector fuerza F y el vector desplazamiento s:
W = F ● s
En el Sistema Internacional las unidades del trabajo son
newton x metro o joules,
que se abrevia J.
Como el producto
escalar entre dos vectores equivale a multiplicar sus magnitudes por el coseno
del ángulo θ que hay entre ellos, el trabajo queda:
W = F.s.cos θ
A partir de esta expresión podemos hacer una observación
importante:
Una fuerza realiza
trabajo sobre un objeto siempre y cuando tenga una componente en la misma
dirección del movimiento.
Ahora se explica por qué la normal no hace trabajo sobre los
objetos que se mueven sobre una superficie. Y es que la normal y el
desplazamiento siempre forman un ángulo de 90º, y como cos 90º = 0, resulta que
la normal, en efecto, no hace trabajo.
Entonces podemos establecer que:
Si una fuerza actúa en
dirección perpendicular al desplazamiento que experimenta el objeto, dicha
fuerza no hace trabajo mecánico.
Podemos contemplar otros casos importantes:
-Trabajo hecho por una fuerza paralela al desplazamiento: si
el ángulo entre F y s es 0º, el trabajo realizado por F es
máximo.
W = F.s . cos 0º = F.s
Por ejemplo el peso cuando actúa sobre un objeto que cae
libremente.
-Trabajo hecho por una fuerza opuesta al desplazamiento: si
el ángulo entre F y s es 180º, el trabajo realizado por F es mínimo:
W = F.s . cos 180º = - F.s
El roce cinético siempre se opone al movimiento de un
cuerpo, por lo tanto hace trabajo negativo. Asimismo se comporta el peso cuando
tratamos de elevar un objeto.
En la siguiente figura se tiene el diagrama de cuerpo libre
del objeto a la derecha. Sobre él actúan tres (3) fuerzas: la normal N, el peso P y la fuerza F. El
desplazamiento es horizontal de izquierda a derecha.
Como podemos ver, ni la normal ni el peso hacen trabajo
sobre el cuerpo, ya que son perpendiculares a la dirección del vector s. En cambio, la componente horizontal
de F es la que se encarga de hacer
trabajo sobre el cuerpo, favoreciendo su desplazamiento en la dirección
indicada.
 |
| Figura 2. La normal y el peso no hacen trabajo sobre el objeto cuando se mueve de esta forma. Fuente: F. Zapata. |
El trabajo que hace F viene dado por:
WF = Fx.s = F.s.cos θ
Ejemplo 1Supongamos que sobre el objeto de la figura 2 actúa una fuerza constante cuya magnitud es de 48 N, formando un ángulo de 60º con la horizontal. ¿Cuál es el trabajo que esta fuerza realiza sobre el cuerpo si este recorre una distancia de 5 m sobre la superficie horizontal? SoluciónAplicando la definición de trabajo se tiene:
W = 48 N. 5 m. cos 60 º = 120 J. Trabajo hecho por una fuerza variable
Si la fuerza es variable, o si el ángulo entre ella y el desplazamiento
no es constante porque la trayectoria es curva, se toma un desplazamiento
diferencial ds y se determina cuál
es el trabajo realizado:
dW = F. ds
Para calcular la contribución al trabajo dW cuando el objeto
viaja desde el punto A hasta el punto B se integra:
La fuerza que ejerce un resorte sobre un objeto atado en uno
de sus extremos es un buen ejemplo de fuerza variable. Recordemos que para
pequeños desplazamientos, se cumple la ley de Hooke para el resorte, según la
cual, la fuerza que este ejerce sobre el objeto es proporcional a su elongación.
Variación en la energía de un sistema
La energía de un sistema cambia cuando hay fuerzas externas
actuando sobre él y hacen trabajo. Entonces podemos relacionar la variación en
la energía con el trabajo hecho por las fuerzas externas de esta manera:
Variación en la energía del sistema = Trabajo hecho por las
fuerzas externas
Sea DE la
variación en la energía y Wext
el trabajo hecho por la fuerza externa, entonces:
DE = Wext
Cuando hay más de una fuerza externa, el trabajo se expresa
como el trabajo neto, el cual no es otra
cosa que la sumatoria de los trabajos que cada fuerza hace sobre el
cuerpo:
Wext
= W1 + W2 + W3 + … = ∑ Wi
Si las fuerzas hacen trabajo tal que se añade energía al
sistema, entonces W>0 y cuando sucede a la inversa, si las fuerzas restan
energía W<0.
En caso de que la energía permanezca inalterada, entonces DE = 0
y puede pasar que:
-El sistema está aislado y por consiguiente ninguna fuerza
externa actúa sobre él.
-Sí hay fuerzas externas, pero son perpendiculares a la dirección
del movimiento.
Como el trabajo realizado equivale a la variación de la
energía, esta tiene las mismas unidades que el trabajo. Es decir, las unidades
de la energía en Sistema Internacional son los joules.
Teorema trabajo-energía
cinética
Cuando un objeto tiene movimiento, posee una forma
particular de energía asociada a este, que es la energía cinética. Sea K la
energía cinética de un objeto cuya masa es m
y que se mueve con rapidez v:
K= ½ mv2
De la definición quedan claros dos aspectos importantes:
-Si un objeto está en reposo, no tiene energía cinética. Pero
puede tener otras formas de energía, como energía potencial gravitatoria, si se
encuentra a cierta altura sobre el suelo.
-La energía cinética no puede ser una cantidad negativa, ya
que la masa y el cuadrado de la rapidez son positivos siempre.
¿Cómo cambiar la energía cinética de un objeto? De varias
formas: cambiando su rapidez, cambiando su masa o ambas a la vez. En muchos
casos la masa permanece constante y es la rapidez lo que cambia, como en el
caso de un balón de fútbol cuando es pateado, pero en otros la masa cambia,
como en el caso de un cohete.
En todo caso hace falta un trabajo neto para cambiar la
energía cinética de un cuerpo, por lo tanto, podemos afirmar que:
Wneto = DK
A esta expresión se la conoce como teorema trabajo-energía
cinética. Y en pocas palabras dice que el cambio producido en la energía cinética
de un cuerpo se debe al trabajo neto que se ha realizado sobre él.
Antes se dijo que la energía cinética siempre es positiva,
pero su variación puede ser positiva o negativa según el curso de los sucesos.
Como la variación se puede expresar como la diferencia entre la energía cinética
final y la inicial, podemos escribir:
DK = Kfinal
– K inicial
Si Kfinal
> K inicial, las fuerzas añadieron energía al sistema y DK > 0. Pero si Kfinal < K inicial
el sistema cedió energía al entorno y la variación en la energía es negativa: DK
< 0.
Energía cinética de diversos
objetos en movimiento
Figura 2. La energía cinética del vehículo depende de su masa y del cuadrado de su velocidad. Fuente: Pixabay.
Ejemplo 2
Una
roca vuela por el aire a 12,4 m/s con una energía cinética de 305 J. Calcular:
a) Su
masa
b) Su
energía cinética si la rapidez se duplica.
c) La
energía cinética si la rapidez disminuye a la mitad.
Solución a
K= ½ mv2
Por lo tanto:
m = 2K/v2 = 2 . 305 J/ (12,4 m/s)2 =
3.97 kg.
Solución b
Si la rapidez se duplica, la nueva energía cinética es:
K = ½ m(2v)2= 4 [½ mv2]
Lo que significa que la energía cinética se cuadruplica,
entonces su valor será: 4 x 305 J = 1220 J.
Solución c
Cuando la rapidez disminuye a la mitad:
K = ½ m(v/2)2= [ ½ m(v)2]/4
La energía cinética disminuye a una cuarta parte del valor
original, por lo tanto el nuevo valor es K = 305/4 J = 76.25 J.
Ejemplo 3
Una
partícula de masa m está
sujeta a una fuerza que actúa en la dirección x, Fx
= (3.0 + 0.50x)
N. Calcular el trabajo realizado por la fuerza cuando la partícula se mueve de x = 0 a x = 4.0 m.
Solución
Se trata de una fuerza variable, por lo tanto:
|
Como la fuerza está dirigida a lo largo del eje x:
Por F. Zapata
Referencias
- Bauer, W. 2011. Física para Ingeniería y Ciencias. Volumen 1. Mc Graw Hill.
- Figueroa, D. (2005). Serie: Física para Ciencias e Ingeniería. Volumen 2. Dinámica. Editado por Douglas Figueroa (USB).

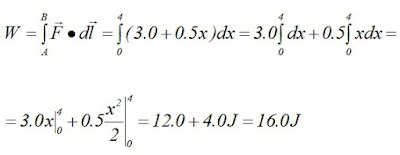
No hay comentarios:
Publicar un comentario