Las fuerzas de rozamiento

 

Las fuerzas de rozamiento aparecen siempre entre superficies en contacto, por ejemplo, entre dos superficies sólidas, o entre una superficie y un fluido, como agua o aceite. Hacen su aparición ya sea que exista o no movimiento entre las superficies en contacto.

Se trata pues, de fuerzas de contacto, por eso son muy importantes y bienvenidas cuando se trata de caminar, correr, rodar, frenar vehículos o sujetar objetos, y no tanto en lo que se refiere a mecanismos, ya que tienden a causar desgastes entre las partes en contacto.

Sin las fuerzas de roce entre la suela y el pavimento no sería posible caminar. Fuente: Pixabay.

Suelen estudiarse dos tipos de fricción: la fricción seca, que como su nombre indica, ocurre entre superficies en contacto secas, y la fricción viscosa, si hay interpuesta una capa de fluido, como aire, agua o aceite, entre las superficies en contacto. En este post se hará referencia a la fricción seca.

El origen de la fricción seca

El rozamiento surge principalmente de las irregularidades microscópicas que poseen todas las superficies, por más pulidas y lisas que parezcan a simple vista. De esta forma, se producen en ellas diminutas crestas y valles. Cuando una superficie intenta moverse, las irregularidades se enganchan unas con otras, lo cual supone una dificultad para el movimiento.

Para que este se produzca, se deben salvar estas pequeñas irregularidades. Sin embargo, la cosa es más compleja que esto, ya que si las superficies están en reposo mutuo, pueden surgir incluso enlaces entre las moléculas de una y otra, lo cual contribuye al agarre entre ambas.

En la siguiente imagen se ilustra lo dicho. A la izquierda hay un cajón pesado, el cual se desea mover de izquierda a derecha sobre la superficie con rozamiento. Una ampliación de lo que sucede en un punto de contacto muestra las irregularidades en las superficies, que se enganchan unas con otras, dificultando el movimiento (o impidiendo que el cajón se desplaze, todo depende de lo que se quiera).

Entre la superficie del cajón y la del suelo existen pequeñas irregularidades que se enganchan una a la otra, lo que origina una fuerza de agarre entre ambas superficies. Fuente: Open Stax Physics Course.

Si el movimiento deseado es de izquierda a derecha, como lo señala la flecha de color negro en la figura, entonces el rozamiento f se dirige de derecha a izquierda, es decir, se opone al movimiento, ya sea que este se haya establecido, o que solamente se pretenda mover el cajón.

¿Qué pasaría si se desea mover el cajón de derecha a izquierda? Pues que el rozamiento se opone a esta intención de movimiento y cambia su sentido, pero, en todo caso, la fuerza siempre será tangencial (paralela) a las superficies en contacto.

Tipos de fricción entre superficies secas

Cuando se habla del rozamiento, hay que distiguir dos situaciones, la primera ocurre cuando las superficies están en reposo mutuo, como lo saben quienes han tratado de acomodar el lápiz sobre la mesa ligeramente inclinada del pupitre, y la segunda, surge si las superficies están en movimiento relativo:

• Roce estático
• Roce dinámico (o cinético)

Cómo calcular la fricción

Experimentalmente se ha determinado que la magnitud de la fuerza de fricción máxima entre dos superficies en contacto es proporcional a la de la fuerza normal existente entre ellas, su dirección es paralela a las superficies y su sentido es opuesto al movimiento, o a la intención de movimiento, en caso de que los objetos se encuentren en reposo.

En primera instancia, dicha magnitud es completamente independiente del tamaño de las áreas en contacto, y también de la velocidad con que se mueve una superficie respecto a la otra. A este resultado, válido para dos superficies secas en contacto mutuo, se le conoce como la ley de Coulomb del rozamiento (no confundir con la ley de Coulomb para la fuerza eléctrica, acá está el link).

Ahora bien, al momento de calcular, hay que distinguir entre el roce estático y el roce dinámico o cinético.

Fricción estática

 Esta fuerza surge cuando las superficies en contacto están en reposo una respecto a la otra.

Supóngase que el cajón de la figura está quieto sobre la superficie. Si no hay fuerza externa alguna que pretenda mover horizontalmente el cajón, la fricción estática es nula.

Pero si a alguien se le ocurre tratar de empujar el cajón, la magnitud de la fricción estática va aumentando de a poco hasta alcanzar el valor máximo, en el momento justo en que va a producirse el movimiento.

Este valor máximo, de acuerdo con la ley de Coulomb del rozamiento, es proporcional a la magnitud de la normal. Llamando f_s a la fuerza de rozamiento y f_s a su magnitud, se puede expresar lo antes dicho en forma matemática mediante:

0 ≤ f_s ≤  (f_s)_max

Y además,  la ley de Coulomb del rozamiento asegura que:

(f_s)_max ∝ N 

La igualdad se establece mediante una constante de proporcionalidad llamada coeficiente de roce estático μ_s.

De esta forma:

1) (f_s)_max = μ_s ∙N 

Como se puede ver, el coeficiente de rozamiento estático es una cantidad adimensional, cuyo valor dependerá de cómo son las superficies en contacto, por ejemplo, metal-madera, plástico-madera, metal-hielo y así. Hay tablas para encontrar estas cantidades, las cuales se determinan experimentalmente.

Fricción cinética

Siguiendo con el ejemplo del cajón que se mueve sobre una superficie, si la fuerza externa se impone ante la fricción estática, el cuerpo se mueve y la fricción pasa a convertirse en fricción cinética, a la cual llamaremos f_k y que, en principio, mantiene constante su magnitud durante todo el movimiento.

En este caso la constante de proporcionalidad cambia y pasa a llamarse coeficiente de roce cinético μ_k, que también es adimensional, pero cuyo valor es menor que el del coeficiente de fricción estática. Todos han observado que es más fácil mantener un objeto en movimiento que comenzar a moverlo, y esto ocurre porque el coeficiente de roce cinético siempre es menor que el estático.

Posiblemente esto se debe a que, cuando las superficies están en reposo mutuo, surgen entre ellas ciertos enlaces iónicos, los cuales favorecen el agarre. Después, estos enlaces desaparecen en cuanto se inicia el movimiento.

Por lo tanto, puede afirmarse que:

f_k < f_s

Ahora la magnitud de la fuerza de roce cinético puede calcularse a través de la fórmula:

2) f_k = μ_k ∙N 

 El comportamiento de la fricción f versus la fuerza externa F_ext antes descrito puede sintetizarse en la siguiente gráfica. A las respectivas magnitudes se las ubica así: la de f en el eje vertical, mientras que la de F_ext, con la cual se pretende mover al objeto, está en el eje horizontal.

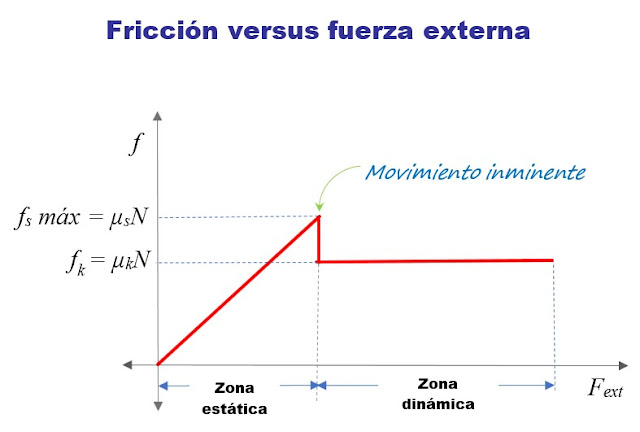Comportamiento del roce ante la aplicación de una fuerza externa. Fuente: F. Zapata.

Hay dos regiones diferenciadas, la primera es la zona estática, donde aún no se produce el movimiento, mientras que la segunda es la zona dinámica, en la cual el objeto ya se mueve. Nótese que en la primera zona, la fuerza de fricción va creciendo linealmente con la fuerza aplicada hasta llegar al máximo, justo cuando el movimiento es inminente. Hasta aquí actúa la fricción estática.

Después la magnitud de la fuerza de fricción decrece, toma el nombre de fricción dinámica y se mantiene constante mientras dura el movimiento.

Resumen de las características del rozamiento entre superficies secas

1. La magnitud de las fuerzas de rozamiento seco es independiente del tamaño del área de contacto y de la velocidad de las superficies, y es proporcional a la magnitud de la fuerza normal.
2. La dirección del rozamiento siempre es paralela a la superficie que la ejerce.
3. El sentido de la fuerza de roce es opuesto al movimiento o a la intención de este.
4. La magnitud del rozamiento está entre 0 y un valor máximo que depende de las superficies en contacto.
5. El coeficiente de roce estático es mayor que el coeficiente de roce cinético.

Ejemplo resuelto

Un esquiador, cuya masa es de 67 kg está esquiando sobre una cuesta con rozamiento, cuya inclinación respecto a la horizontal es de 37º. 

Calcular:

a) La magnitud de la fuerza de fricción si se sabe que el coeficiente de fricción cinética entre la superficie de los esquíes y la nieve es 0.07.

b) La magnitud de la aceleración del esquiador al descender por la cuesta.

Un esquiador desciende por una cuesta, tomando en cuenta el efecto de la fricción. A la derecha está el diagrama de cuerpo libre. Fuente: Open Stax Physics Course. Modificado por F. Zapata.

Solución a

 En la figura de arriba está el diagrama de cuerpo libre. Las consideraciones para resolverlo son las mismas que las de la máquina simple llamada plano inclinado, aquí está el link del paso a paso para resolver el problema del plano inclinado.

Será preciso aplicar las leyes de Newton y el primer paso, como siempre es encontrar las componentes del peso, que es la única fuerza inclinada, según el sistema de coordenadas seleccionado.

La magnitud del peso del esquiador es:

W = mg = 67 kg∙ 9.8 m/s² = 656.6 N

De acuerdo al diagrama de cuerpo libre, las componentes del peso son:

W_x = mg∙ sen 37º = 656.6 N∙sen 37º = 397.0 N

W_y = mg∙ cos 37º = 656.6 N∙cos 37º = 524.4 N

Aplicando la segunda ley de Newton se tiene:

•  ∑ F_y = N - W_y = 0
•  ∑ F_x = f_k – W_x = ma_x

De la primera ecuación se despeja la magnitud de la normal:

N = W_y = 524.4 N

Y al aplicar la ecuación 2), dada más arriba para el cálculo de la fricción cinética, se obtiene:

f_k = μ_k ∙N = 0.07 ∙524.4 N = 36.7 N

Solución b

De la ecuación 2 se despeja a_x :

El resultado es negativo, no hay problema con ello, pues en el diagrama de cuerpo libre se ha tomado como sentido positivo de las x al de la fricción (cuesta arriba). Ya que el esquiador desliza cuesta abajo, su aceleración tiene signo negativo.

 Por F. Zapata