Con
frecuencia las estructuras están sujetas a la acción de una serie de fuerzas
paralelas y en la misma dirección, pero cuya intensidad siempre es la misma en
cada uno de sus puntos.
Por ejemplo
considérese el peso de un cuerpo. Si imaginamos que el cuerpo está constituido
por numerosas partículas, cada una de ellas es atraída hacia el centro de la
Tierra con una determinada fuerza. Al sumar todas estas contribuciones,
paralelas y apuntando hacia el suelo, se tendrá el peso del objeto.
 |
| La nieve que se acumula sobre los tejados ejerce sobre estos una fuerza distribuida sobre toda la superficie. Fuente: Pixabay. |
Normalmente
no se dibujan todas estas pequeñas fuerzas, ya que el número de partículas que
componen el cuerpo es innumerable. Si el objeto tiene una forma geométrica
regular, el peso se dibuja aplicado en su centro geométrico, y si la forma no
es regular, el peso se dibuja aplicado en el centro de gravedad del cuerpo.
Otro
ejemplo de fuerza distribuida es la que ejerce el agua de una piscina sobre una
de las paredes o sobre el fondo. El fluido ejerce una presión sobre el fondo, a
través de una fuerza que es perpendicular a la superficie, está dirigida hacia
abajo y tiene igual magnitud, algo así como lo que se muestra en esta figura. Pero en una
superficie lateral es diferente, ya que la fuerza aumenta conforme lo hace la
profundidad. Entonces, la fuerza en la superficie del agua es nula, y es máxima
en el fondo de la piscina. Más
ejemplos de fuerzas distribuidas son la fuerza del viento sobre la fachada de
una edificación, la que ejerce la nieve que ha caído sobre un tejado o la que
hace un pilar sobre su base. Tratar de
encontrar la fuerza resultante sobre la pared lateral de la pisicina sería una
tarea ardua, pues se debería sumar una a una la contribución sobre cada
partícula de la pared. Sin embargo, el cálculo matemático facilita la tarea,
como se verá en los ejemplos. Carga distribuida a lo largo de una vigaObsérvense
las vigas de longitud L, que se muestran a continuación. Las fuerzas sobre
ellas son verticales, pero se distribuyen de forma diferente a lo largo.
El conjunto de vectores fuerza que actúan sobre la viga es lo que se conoce como un campo
vectorial de fuerzas. En la
imagen izquierda, las fuerzas que actúan sobre la viga tienen la misma
magntitud y sentido, además, están aplicadas de manera homogénea sobre toda la
longitud, por eso se llama carga uniformemente distribuida, porque la
fuerza tiene la misma intensidad a todo lo largo. En la
figura derecha, las fuerzas son verticales y hacia abajo, pero no tienen la
misma magnitud, sino que esta crece de izquierda a derecha, partiendo de 0 en
el lado izquierdo y alcanzando un máximo en el lado derecho de la viga. La
figura que se forma es un triángulo, y por eso es una distribución de carga
triangular. Naturalmente,
la carga puede distribuirse de otras maneras, aparte de estas. Pero en
cualquiera de estos casos, ¿cuál es la fuerza resultante sobre la viga y
dónde se puede considerar que esté aplicada? Sería interesante saberlo, pues la
distribución se puede sustituir por esta resultante y el punto donde se aplica,
y así estudiar mejor sus efectos. Cálculo de la fuerza
resultante
Según el principio de superposición, la fuerza resultante se obtiene al sumar cada contribución. Las figuras muestran un número limitado de estas fuerzas, pero en realidad, ellas actúan sobre cada punto de la viga. |
En la
figura de arriba a la izquierda, se muestra una fuerza distribuida sobre una viga
de longitud L y ancho b. Dicha distribución varía a lo largo del
eje x, que es el eje sobre el que se ubica la viga, siguiendo una curva,
dada por la función p(x), cuyas unidades en el Sistema Internacional son
N/m2, es decir, las mismas unidades de la presión, que viene dada
como fuerza por unidad de área.
Si esta
función p(x) se multiplica por el ancho de la viga, se tiene la fuerza por
unidad de longitud, a la cual se llamará w(x) (figura del medio):
w(x) = p(x)∙b
Supóngase
que se toma una pequeña parte de la viga, de largo dx:
Entonces la fuerza dF sobre esta pequeña parte es el
producto entre w(x) y la longitud dx:
dF = w(x)dx
Lo anterior equivale a una pequeña porción del área bajo la
curva, llamada dA.
Para obtener la fuerza resultante FR, se
suma cada pequeña contribución dF a lo largo de la viga, lo cual da lugar a la
siguiente integral definida:
En otras palabras, la fuerza resultante equivale al área
(sombreada) bajo la curva.
Centro de aplicación de la fuerza
La fuerza resultante calculada en el apartado anterior, cuya
magnitud es F, está aplicada en el punto C, en la figura de arriba
izquierda y derecha. Este punto se llama centro de aplicación de la fuerza,
se denota mediante una “x” con una barra encima, y su ubicación está por
determinarse, con ayuda del momento.
Cada contribución de la fuerza, llamada dF, produce un momento de magnitud xdF
alrededor del punto O, según se aprecia en la figura del centro (recuérdese que
la magnitud del momento viene dada en este caso por el producto entre la fuerza dF y
su distancia x al eje de giro, ubicado en O en este caso).
Sumando cada una de estas contribuciones del momento, se
tiene la magnitud del momento total, respecto a O. Como se sabe, esta suma es una integral:
Pero dF = w(x)dx, entonces:
Y a su vez, esta integral equivale al producto de “x” con barra encima, multiplicado por la magnitud de la fuerza resultante, por lo que es válido escribir:
 |
| Ecuaciones para la resultante de una fuerza distribuida y la localización del punto de aplicación. |
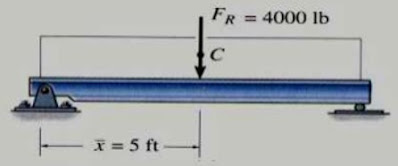
Ejemplo 1
Sobre la viga de longitud igual a 10 pies, mostrada en la figura, actúa una fuerza distribuida uniformemente, con w(x) = 400 lb/pie. Calcular la magnitud de la fuerza resultante y su centro de aplicación.
Solución
Para hallar la fuerza resultante no es necesario integrar,
ya que el área bajo w(x) es simplemente la de un rectángulo de base 10 pies y altura
400 lb/pie, por lo tanto:
FR = 10 pies × 400 lb/pie = 4000 lb
Ejemplo 2
La viga de la siguiente figura tiene L = 6 m, y el valor máximo de la
fuerza por unidad de longitud es 600 N/m. Hallar:
a) La función w(x)
b) La magnitud de la fuerza resultante
c) El centro de aplicación de la fuerza
Solución a
La función w(x) tiene la forma de una recta que pasa por el origen:
w(x) = mx
Donde m es la pendiente de la recta:
w(x) = 100x N/m
Solución b
Conociendo
FR = (6 m × 600 N/m)/2 = 1800 N
Solución c
El centro
de la aplicación de la fuerza coincide con el centroide del triángulo, ubicado
a 1/3 del extremo derecho de la figura, es decir, a 2 m del extremo derecho o
ben a 4 m del extremo izquierdo.
También
puede integrarse, ya que no es difícil y se obtiene el mismo resultado:
Ejemplo 3
Hallar la resultante
de la distribución mostrada arriba y el centro de aplicación de la fuerza:
Solución
Se pueden
superponer tres distribuciones homogéneas. La primera tiene altura 1.5 kN/m y
base 3m, la segunda tiene altura 1 kN/m y base 3 m, y la tercera tiene altura
2.5 kN/m y base 1.5 m:
FR
= (1.5 × 3) kN + (1 × 3) kN + (2.5× 1.5) kN = (4.5 + 3 + 3.75) kN = 11.25 kN
La fuerza neta en cada una se puede suponer
aplicada en su respectivo centro. La primera fuerza, de 4.5 kN se aplica a 1.5
m del punto A, la segunda, de magnitud 3 kN, se aplica a 4.5 m del punto A y la
tercera, de 3.75 kN, se aplica a 6.75 m del punto A.
El momento respecto a A, producido por cada distribución, es entonces:
MA
= (4.5 × 1.5) kN∙m + (3 × 4.5) kN∙m + (3.75× 6.75) kN∙m = 45.5625 kN∙m
Dado que:









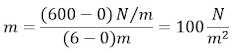




No hay comentarios:
Publicar un comentario