Sistema equivalente fuerza-par

Un sistema de fuerzas, actuando sobre un cuerpo, puede hacer que este se traslade y a la vez rote.  Ambos efectos  pueden ser descritos a través de la acción de una fuerza resultante más un par de fuerzas, que como se sabe, tiene asociado un momento. 

La acción conjunta de esta fuerza más el par, produce sobre el objeto el mismo resultado que el del sistema de fuerzas original, pero es más simple de analizar. Obsérvese cuidadosamente la siguiente figura:

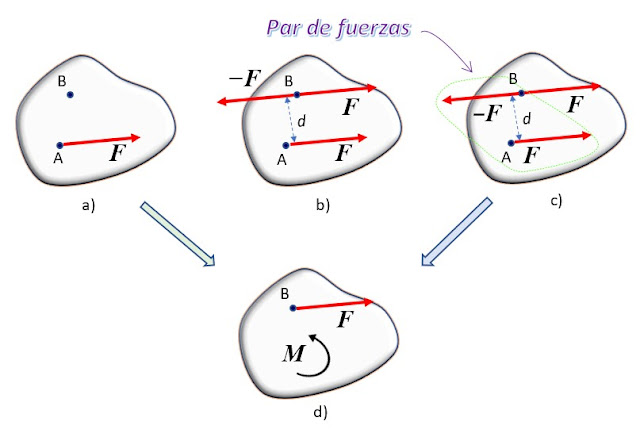La acción de un sistema de fuerzas actuando sobre un objeto, se puede describir como un sistema de fuerza + momento de un par. Fuente: F. Zapata.

La figura a) representa un objeto sobre el cual actúa una fuerza F aplicada en el punto A, mientras que B es otro punto del objeto. Dicha fuerza es el sistema de fuerzas original, que en este ejemplo, consta simplemente de una fuerza única.

En la figura b) se aplican el punto B dos fuerzas de igual magnitud y dirección que F, pero de sentido contrario. Estas fuerzas, llamadas F y – F no constituyen un par, ya que están aplicadas al mismo punto. Pero – F, aplicada en B y F, aplicada en A sí forman un par, siendo d la distancia perpendicular entre ambas líneas de acción (figura c, las fuerzas encerradas en la línea segmentada verde).

Como se recordará, la acción de un par de fuerzas sobre un objeto es la de proporcionar un giro, siendo el momento M la magnitud vectorial encargada de describirlo. Por lo tanto este par se sustituye por el momento M y queda la fuerza F aplicada en el punto B. Este sistema fuerza-par es equivalente a al sistema original.

La fuerza F se encarga de trasladar al cuerpo, mientras que el momento M es responsable de la rotación del mismo.

La utilidad de encontrar un equivalente fuerza-par, radica en que, conociendo la fuerza o el sistema de fuerzas que se aplica sobre el cuerpo en cierto punto, es posible calcular la pareja fuerza-par aplicados sobre otro punto, que equilibre al sistema original. 

Por ejemplo, si se trata de una pieza de mampostería, que se sabe estará sometida en un extremo a cierta fuerza, se puede calcular qué clase de soporte se debe colocar en el otro extremo para que la pieza se mantenga en su lugar, sin caer ni girar.

Veamos a continuación un ejemplo de cómo reemplazar una fuerza, o un sistema de fuerzas, por una fuerza única más un par, cuyo efecto sea equivalente al del sistema original.

Ejemplo 1

Reemplazar la fuerza de magnitud 800 libras mostrada en la figura, por un sistema equivalente fuerza-par en: a) el punto O y b) en el punto B.

Ejercicio propuesto del libro Estática, Meriam-Kraige.

Solución a

Conforme al procedimiento descrito al comienzo, hay que aplicar en O dos fuerzas de magnitud 800 lb, con la misma dirección de la fuerza original, pero con sentidos opuestos (figura a). Como resultado de ello, la fuerza original en A y su opuesta en O dan lugar a un par (figura b).

Para encontrar el momento, se puede emplear cualquiera de los métodos vistos en los post anteriores. Por ejemplo, el coseno del ángulo θ que forma la fuerza F con el eje horizontal es:

Por lo tanto, la magnitud del momento producido por F en el punto O es:

Mediante la regla de la mano derecha o simplemente observando que (−i) × (−j) = k, se deduce que el momento es antihorario.

Solución b

La situación ahora es la siguiente:

En este caso es preferible expresar los vectores de posición y fuerza en términos de sus componentes i y j, y luego llevar a cabo el producto vectorial en forma analítica:

El vector r_AB es:

r_AB = −4 i – 3 j plg

Mientras que el vector fuerza es:

Por lo tanto, el vector momento es:

El momento resultante también tiene sentido antihorario, como en el caso a), pero su magnitud es mayor. 

Ejemplo 2

Tres varillas de control unidas a la palanca ABC ejercen sobre ésta las fuerzas mostradas en la figura. Reemplace las tres fuerzas por un sistema fuerza-par equivalente en B.

Ejercicio propuesto del libro Mecánica Vectorial para Ingenieros. Beer-Johnston.

Solución

 

La fuerza resultante F es, tomando el eje x como se muestra en la figura:

F = 48 (sen 55º i + cos 55º j) lb = (39.3 i + 27.5 j) lb

Si se toma el eje x horizontal, entonces F forma un ángulo de (90-55+30º) respecto a dicho eje. En tal caso:

F = 48 (cos 65º i + sen 65º j) lb = (20.3 i + 43.5 j) lb

Nótese que las fuerzas de 20 lb de magnitud forman un par y por consiguiente su suma vectorial es nula.

Dado que las fuerzas y los vectores de posición están en el plano xy, los momentos estarán dirigidos perpendicularmente a la pantalla (se deja el link donde se explica el producto vectorial, en caso de que sea necesario repasar).

En primer lugar se calcula el momento del par de fuerzas de 20 lb.

M₁ = −20 lb × 70 plg × cos 20^o k = − 1315.6 k lb × plg

Ahora, el momento de la fuerza de 48 lb, respecto al punto B:

M₂ = + 48 lb × 30 plg × cos 55^o k = 826.0 k lb × plg

Por último, la suma vectorial de los momentos:

M_B =  (− 1315.6 k + 826.0 k ) lb × plg = − 489.6 k lb × plg

El signo negativo indica que el momento resultante en B es horario.