El teorema de Varigon, también conocido como el principio de los momentos, establece que:
Dado un
sistema de fuerzas concurrentes, el momento resultante sobre él respecto a un
eje, equivale a la sumatoria de los momentos de las fuerzas aplicadas respecto
a dicho eje.
Originalmente
propuesto por el holandés Simon Stevin (1548-1620), fue el matemático francés
Pierre de Varignon (1654-1722) quien le dio la forma actual, publicándolo por vez primera en 1687
en su obra Nouvelle
mécanicque. Pierre de Varignon también fue un destacado geómetra.
La siguiente figura muestra un sistema de N fuerzas concurrentes actuando sobre un cuerpo. Son concurrentes, puesto que las líneas
de acción de cada una de ellas se cortan en un punto P:
El punto de aplicación de la fuerza F1 es
Q1, el de la fuerza F2 es Q2, el de la
fuerza F3 es Q3 y así sucesivamente. Los vectores
de posición con respecto al sistema de referencia son rOQ1, rOQ2, rOQ3
y así sucesivamente.
Con esta notación, el teorema de Varignon afirma que el
momento respecto al punto O, producido por el sistema de fuerzas es:
MO = rOP × FR
Donde rOP es el vector de posición del punto de concurrencia P de las fuerzas y FR es la fuerza resultante del sistema.
Demostración
Es muy sencillo demostrarlo, ya que el momento resultante se
obtiene a través de la suma vectorial de los momentos producidos por cada
fuerza:
MO = M1 + M2
+ M3 + … MN = (rOQ1 × F1) + (rOQ2 × F2) + (rOQ3 × F3) + … (rOQN × FN)
Pero, hay que observar cuidadosamente
la figura, para ver que el vector rOQ1 (rojo oscuro) se puede expresar como la suma vectorial entre rOP
(verde) y el vector PQ1 (morado), siendo este último paralelo
a la fuerza (de ser necesario, repasar nuevamente el post de suma de vectores, cuyo link se deja acá).
Entonces:
M1 = (rOP + PQ1 ) × F1
La propiedad distributiva también se
puede aplicar al producto vectorial:
M1 = (rOP + PQ1 ) × F1 =( rOP × F1 ) + (PQ1 × F1 )
El producto vectorial PQ1 × F1 es nulo por ser paralelos ambos vectores (verlo en la figura), quedando:
M1 = rOP × F1
Algo similar ocurrirá con M2,
M3 …. MN, entonces:
MO = M1 + M2
+ M3 + … MN = rOP × F1 + rOP × F2 + rOP × F3 +… + rOP × FN = ∑ rOP × Fi = rOP × ∑ Fi = rOP × FR
Que es precisamente el teorema de
Varignon, muy útil para calcular el momento de un sistema de fuerzas
concurrentes, sin necesidad de conocer el vector posición para cada una de las
fuerzas, ya que solo es preciso conocer el vector de posición del punto de
concurrencia y, naturalmente, la fuerza resultante.
Una vez convencidos de que el teorema
es útil y cierto, veamos algunos ejemplos:
Ejemplo 1
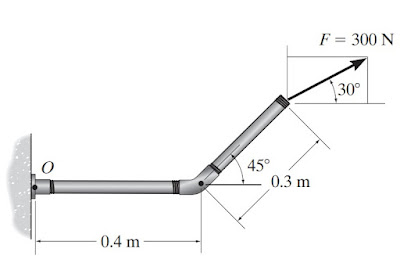
Hallar el momento que ejerce la
fuerza mostrada en la figura, respecto al punto O, empleando el teorema de
Varignon.
Solución
El teorema de Varignon afirma que:
MO = rOP × F
Donde P es el punto de aplicación de la fuerza.
El vector de posición buscado es rOP , que se puede ver como la suma de dos vectores, cuyas componentes se visualizan directamente de la información suministrada en la figura:
rOP = 0.4 m i + 0.3 (cos 45º i + sen 45º j) m = (1.37 i + 0.21 j ) m
Por su parte, la fuerza F es:
F = 300 (cos 30º i + sen 30º j) N = (259.8
i + 150 j ) N
El momento respecto a O es, entonces:
MO = rOP × F = (1.37 i + 0.21 j
) m × (259.8 i + 150 j ) N = (1.37 i × 150 j)
+ (0.21 j × 259.8 i) N∙m =
= (205. 5 k –
54.6 k) N∙m = 150. 9 k N∙m
Ejemplo 2
Hallar el momento que ejerce el
sistema de fuerzas mostrado a continuación, respecto al punto O, empleando el
teorema de Varignon.
Solución
De acuerdo a la figura, las coordenadas del punto A son (3,
3, −2)
pies. Como las coordenadas del origen O se escogen como (0, 0, 0) pies, el
vector que va desde O hasta A es:
rOA = (3i + 3j – 2k) pies
Por su parte, la fuerza resultante es:
FR = F1 + F2
= (–20i + 10j + 30 k) lb + (–10i – 30j + 50 k)
lb = (–30i – 20j + 80 k) lb
De acuerdo al teorema de Varignon, el momento respecto a O
es:
MO = rOP × F = (3i + 3j – 2k) pies × (–30i – 20j + 80 k) lb
Que se calcula fácilmente con el método del determinante (abrir el link para repasar, en caso de ser necesario):
MO = (200 i – 180 j + 30 k ) lb-pies




No hay comentarios:
Publicar un comentario